Multiwfn FAQ

December 23, 2018, 3:29 pm

≫ Next: 使用CYLview绘制高质量分子结构图和制作化学反应演示动画（视频演示）

Multiwfn FAQ

First release: 2018-Dec-24 Last update: 2018-Dec-28

波函数分析程序Multiwfn（http://sobereva.com/multiwfn）如今已十分流行，本文针对用户常问的问题进行统一解答，也推荐所有Multiwfn用户完整阅读此文，此文会经常更新。本文分为四部分：(1)常识性问题 (2)安装、配置、运行问题 (3)一般使用问题 (4)和图像显示、绘图有关的问题。

1 常识性问题

Q1：Multiwfn是干什么的？有什么功能？
A：量子化学程序计算之后会产生电子波函数，Multiwfn属于后处理程序，主要功能是对波函数进行分析，从而获得重要、丰富的对研究化学问题十分有益的信息。Multiwfn也提供不少其它对量子化学研究起到帮助的功能。请仔细阅读《Multiwfn波函数分析程序的意义、功能与用途》（http://sobereva.com/184），此文对Multiwfn有较全面的介绍。

Q2：Multiwfn怎么引用？
A：在主页的Download栏目、手册第一章、程序启动一开始显示的信息中、程序压缩包解压后的LICENSE.txt文件里、入门贴《Multiwfn入门tips》（http://sobereva.com/167）中都写明了，不按照要求引用的用户在未来会被纳入黑名单。Multiwfn不收费，而且其开发不拿纳税人一分钱，恰当引用Multiwfn是开发者对用户的唯一要求。

Q3：求Multiwfn程序！求Multiwfn手册！
A：求人不如求己。去官网http://sobereva.com/multiwfn的download页面自行下载，不要钱，不需要注册。忘了官网地址时用google搜Multiwfn，第一条就是。一般用户只需要下文件名末尾是bin的包，里面是可执行程序。manual这个词是手册的意思。

Q4：Multiwfn怎么学？
A：Multiwfn的学习资源异常丰富，极少有计算化学程序有这么多、这么深入浅出的相关学习资源，也极少有程序手册写得像Multiwfn这般详细、贴心、易懂。而且Multiwfn本身也及其易用，没什么门槛。所以不要说什么“不会用Multiwfn”，不会用的前提一定是根本没有拿出哪怕几分钟时间去试图找相关的资料。

自学Multiwfn极其容易。首先务必读《Multiwfn入门tips》（http://sobereva.com/167）和《Multiwfn波函数分析程序的意义、功能与用途》（http://sobereva.com/184）以及本文，以了解Multiwfn相关的基本知识。然后针对自己要做的具体分析，在《Multiwfn入门tips》中的Multiwfn相关博文汇总里看有没有和自己做的分析直接对应的博文，或者看Multiwfn手册第四章提供的相应例子。Multiwfn手册第四章提供了上百个例子，所有Multiwfn比较常用的功能在里面都有示例。Multiwfn的所有功能的原理和程序实现在手册第三章相应章节也都有非常详细的介绍。要注意Multiwfn的功能极多，用法极其灵活，千变万化，一定要在博文和手册例子基础上充分举一反三。为了帮助一些理解能力差或者极度不情愿看文字学习的用户，笔者针对部分主题还专门录了一些简短的Multiwfn使用演示视频，汇总见http://sobereva.com/video.html。此外，强烈建议平时多去Multiwfn论坛看看，Multiwfn任何有关的新资源都会在那里发布，通过阅览其它用户的帖子也可以增进理论和程序使用水平。

有条件的话，非常建议参加北京科音自然科学研究中心每年举办的波函数分析与Multiwfn程序培训班。波函数分析的理论、应用以及Multiwfn的详细使用都会全面、系统地介绍，可以一次性彻底学通。培训时间安排见http://www.keinsci.com，内容介绍见http://www.keinsci.com/workshop/WFN_content.html，往届信息见http://bbs.keinsci.com/forum.php?mod=forumdisplay&fid=43&filter=typeid&typeid=247。

Q5：有问题怎么求助？
A：最佳的求助方式是在Multiwfn论坛发帖。在Multiwfn中文论坛http://bbs.keinsci.com/wfn发帖也行，在Multiwfn英文论坛http://sobereva.com/wfnbbs发帖也行，一般笔者会在一天内回复。如果你周围有外国Multiwfn用户，在他们遇到问题时，希望你能建议他们到Multiwfn英文论坛提问。如果你的问题实在很私密，迫不得已实在没法发到论坛上，也可以给Multiwfn开发者发邮件，邮件地址在Multiwfn启动时就显示了。不建议在任何其它地方咨询Multiwfn的问题，否则基本不可能获得Multiwfn开发者的回复。
求助的时候注意尽可能把情况交代清楚、详细。问的问题表述含糊不清、没有提供对解决问题有效的信息的话，只会耽误获得有效解答的时间。

Q6：有没有使用Multiwfn做xxx分析的博文？以前看过xxx博文，找不到链接了怎么办？
A：去《Multiwfn入门tips》（http://sobereva.com/167）给出的Multiwfn相关博文列表里找。在笔者的博客的索引页面http://sobereva.com/list.html里也可以直接通过相应词语试图搜索有无相关博文。
并不是Multiwfn的各个功能笔者都写过相应的博文，博文绝对代替不了手册，二者目的不同。一些不是很值得专门写博文的内容笔者不会去写博文。没有找到相关博文的时候必须看手册，手册里绝对有每个功能的非常详细的介绍，大部分功能也都提供了例子。

Q7：有没有Multiwfn中文手册？
A：Multiwfn是面向全世界用户的程序，自然手册是英文的，认真阅读《Multiwfn入门tips》（http://sobereva.com/167）后就不会再问这个问题了。Multiwfn手册内容极多，更新非常频繁，开发者没精力同时维护英文和中文两个版本手册，更何况Multiwfn手册里根本没有各种复杂的形容词、副词、句式，比高考阅读理解题简单太多了。

Q8：有没有使用Multiwfn做xxx分析的文章可以给我作为例子？
A：一个简单方法是用Google学术搜索搜，比如想找用Multiwfn绘制DOS的文章，可以试图搜“Multiwfn DOS”（尽管这样并不可能搜出来所有用Multiwfn绘制DOS的文章）。另一个方法是去Multiwfn官网cited by页面下载以往使用了Multiwfn发表的文章的pdf文件合集，然后用acrobat的对某个文件夹里的所有pdf文档进行全文搜索的功能进行搜索。

Q9：Multiwfn能支持什么程序？
A：Multiwfn的绝大部分分析功能都能支持几乎所有知名量子化学程序，如Gaussian、ORCA、Molpro、NWChem、GAMESS-US、Dalton、PSI4等等。有极少数分析只能支持Gaussian等特定程序。Multiwfn目前没法对第一性原理类程序比如VASP、Quantum-Espresso、CP2K等等产生的波函数进行分析，但有很多只需要几何坐标的分析，是可以基于这些程序优化出的结构来分析的，比如IGM分析、Hirshfeld surface分析、promolecular近似下的RDG分析、EEM电荷计算、原子配位数计算等等。

Q10：Multiwfn支持Dmol3、ADF程序么？
A：Multiwfn永远、绝对不会支持又贼贵又严重非主流的Dmol3和ADF！！！！！！！！！Multiwfn只支持高斯型基函数，这是所有主流量化程序用的基函数形式，而Dmol3和ADF分别利用数值型基组和STO型基组，注定不可能被Multiwfn支持，也极少有其它第三方波函数分析程序能支持这俩程序。

Q11：用Multiwfn做xxx分析应该用什么文件作为输入文件？怎样产生？
A：这点在《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》（http://sobereva.com/379）里解释得非常清楚。

Q12：目前的Multiwfn相比之前版本有哪些更新？
A：看Multiwfn官网Update history页面。从1.0版到目前最新版本的所有更新都列在那了。

Q13：Multiwfn相关博文里提及的一些选项怎么在我用的Multiwfn里没有？怎么结果和博文里的不同？
A：是因为你用的Multiwfn版本太老。在博文里通常会说明此博文用的Multiwfn版本，如果你用的版本是更老的，那很可能没有这个功能，或者结果、输出和博文里的不符。要注意Multiwfn程序的更新极度频繁，官网上download页面里文件名带着(dev)后缀的版本是开发版(development version)，开发版甚至有时候一两天就更新一次。比如博文里说的是“本文用的是2018-Nov-20更新的3.6(dev)版”，那你如果用的是2018-Nov-20之前下载的3.6(dev)版就很可能情况和博文不符。Multiwfn程序刚启动的时候屏幕上会明确提示当前的版本是几几年几月几号更新的版本。

Q14：Multiwfn怎么念？
A：见《Multiwfn程序名读法的统一说明》（http://bbs.keinsci.com/thread-11011-1-1.html）。

2 安装、配置、运行问题

Q15：Multiwfn怎么安装？
A：Windows版不用安装直接用。Linux下的安装方法在手册2.1.2节写明了。

Q16：我用的Windows，双击Multiwfn.exe启动后是一个黑乎乎的窗口...我，我，我该怎么做？是不是中毒了？是不是进入黑客模式了？要在里面编程吗？
A：莫慌！这叫命令行(command-line)窗口。Multiwfn不是纯图形界面程序（好处是又方便开发，又便于写脚本批处理，又不是必须依赖于图形环境才能使用），只有需要图形化展现数据的时候才会提供图形窗口。使用Multiwfn时总要睁大眼睛仔细看屏幕上每一个提示，接下来该干什么、有什么选项可以选、该以什么格式输入都提示得超级清楚，连输入例子都给了（e.g.后面的内容），无比贴心！绝对不要把屏幕上的英文当做人类无法阅读的乱码，那些提示信息的用词和语法比高考英语都容易，有个别不懂的用电子词典翻译即可，Multiwfn不可能做成中文界面的程序。Multiwfn手册和博文里的例子把每一步要敲的命令和每一步操作的含义都写得超级详细，不会操作时起码先照着例子敲一遍。

Q17：计算时并行核数和内存怎么设？设多少合适？
A：Multiwfn计算时并行的线程数通过settings.ini里的nthreads来设，建议等于当前机子CPU的物理核心数，这样速度最快。不懂啥叫物理核心和逻辑核心的话看《正确看待超线程(HT)技术对计算化学运算的影响》（http://sobereva.com/392）。
Multiwfn没有一般意义上的内存使用上限设置，当前任务该需要多少内存就会试图用多少内存，如果机子内存不足（物理内存+虚拟内存的总和）就会崩溃；你若用的是32bit Windows版，Multiwfn至多只能用2GB内存，需要的内存量超过这个值时也必然崩溃。
在并行计算时需要考虑所谓的OpenMP stacksize内存设置。Multiwfn通过OpenMP方式进行并行计算，有些变量和数组是每个线程私有的，私有部分最多能利用多少内存取决于settings.ini里的ompstacksize设置，如果这个设得不够大的话也会崩溃。除非遇到OpenMP stacksize内存不足而报错，否则不需要改ompstacksize，改大了也不会令计算速度有任何提升。ompstacksize与nthreads的乘积绝对不能超过剩余物理内存量，内存实在不够的话可以索性将nthreads降低以令ompstacksize能够设大。

Q18：程序启动时出现找不到settings.ini的警告怎么办？
A：Multiwfn每次启动时会试图载入settings.ini里的设置。Multiwfn首先在当前目录下寻找settings.ini，如果找不到，则会在Multiwfnpath环境变量设定的目录下找settings.ini，如果还找不到，则会使用默认设定（和settings.ini里的默认设置相同）。
在Linux下启动Multiwfn时通常不是在Multiwfn目录下启动的，因此对于使用bash shell的用户，应当在用户主目录下的.bashrc中加入比如export Multiwfnpath=/sob/Multiwfn_3.6_bin_Linux，之后重新进入终端即生效。

Q19：Linux下启动Multiwfn时提示version `GLIBC_x.xx' not found报错
A：这说明你的操作系统太老，系统里的GLIBC库的版本低于x.xx。这需要你装更新版本的Linux系统。网上也有直接升级操作系统的GLIBC库的方法可以尝试，但对于不很熟悉Linux的人有一定风险。你也可以自行在当前的机子上编译Multiwfn源代码，这样编译出来的肯定能在你机子上用。

Q20：怎么进入某些功能时提示Can't open X Windows display而自动退出？
A：这说明Multiwfn此时试图显示图形，但你当前的环境是纯文本环境，因此没法显示出图形所致。如果你是通过一般方式的ssh登录远程服务器，或者你的Linux机子是在比如init 3模式下，那么Multiwfn所有涉及显示图形的功能都用不了。

Q21：Linux下运行出现Segmentation fault报错怎么解决？
A：有以下可能原因：
(1)没有严格按照手册2.1.2节的方式配置Linux。Ubuntu、Linux Mint等Linux系统的用户漏了设置ulimit -s unlimited这一步几乎一定会导致这种报错。
(2)输入文件或者操作有问题
(3)Multiwfn与你的操作系统有兼容性问题，或者是Multiwfn的bug。首先尝试Multiwfn最新版本，还不行的话尝试把nthreads设为1，即不用并行方式运行看能否解决。还不行的话尝试用其它Linux发行版运行试试，Multiwfn的Linux版测试都是在CentOS上进行的，对Redhat/CentOS支持是最理想的。也可以改用Windows版试试，或者在你的Linux机子下自行编译Multiwfn并运行试试。

Q22：Windows下，在Multiwfn调用Gaussian计算时，提示“No executable for file l1.exe”错误
A：按照手册附录1说的，设置GAUSS_EXEDIR环境变量，将之指向Gaussian目录即可。

3 一般使用问题

Q23：Windows下使用Multiwfn中途为什么有时会闪退？
A：那是因为用户是通过双击Multiwfn图标启动的程序，当程序出错而崩溃时，运行窗口就会自动关闭，不明真相的用户总是形象地将这描述为“闪退”（笔者不喜欢这种称呼，客观地描述为“窗口突然关闭”多好）。如果你先进入操作系统的命令行模式再启动Multiwfn（在Windows下按住shift再点鼠标右键，就可以通过相应选项进入命令行模式），即便程序崩溃也不会导致命令行窗口自动关闭，此时从窗口上显示的一些信息有助于了解是因为什么而出错（看不懂的话可以让开发者看）。
Multiwfn崩溃的常见原因有：
1 用的输入文件类型不合理。应仔细看手册相关章节或相关博文里对输入文件要求的说明，别瞎猜着用。
2 输入文件残缺不全（诸如文件没传完整），或者输入文件里有诡异信息（诸如本该是数据的地方由于程序bug等原因输出的却是一堆星号），或者载入的文件内容的格式不符合要求。
3 在Multiwfn里的操作步骤不对。每一步操作都要仔细看屏幕上的提示。如果是新手应先把手册或博文里相关的例子完整重复一遍以确保操作方式正确。
4 敲入的内容荒谬、不符合格式要求。诸如逗号误写成了全角的，提示该写空格的地方写的却是逗号，输入的原子、轨道等序号超过实际范围，该输入两个数值的地方输入了三个数值等等。
5 内存不足。如果用的是32bit Windows版，首先换成64bit Windows版再试。也可尝试加大settings.ini里的ompstacksize。如果是Linux版，若没有按照手册2.1.2节的过程安装，也可能由于可用的内存被严重限制住而导致这个问题。实在不行就把体系用的基组减小或想办法减少体系的原子数。
6 程序bug或兼容性问题。先尝试Multiwfn官网上的最新版本，如果通过反复测试能确认最新版本也有这个bug，把压缩后的输入文件、每一步敲入的命令、当前的操作系统版本发到Multiwfn官方论坛，笔者会很快回复。

Q24：怎么把Multiwfn文本窗口里的数据拷出来？
A：仔细看手册5.4节。

Q25：Multiwfn在窗口里输出的信息的靠前部分看不到，即便滚动条拉到头也看不全怎么办？
A：仔细看手册5.5节，加大窗口缓冲区即可。或者通过命令行方式运行，把输出信息都定向到指定的文件里。

Q26：载入文件时敲输入文件路径麻烦，有没有更简单的办法？
A：看《将文件快速载入Multiwfn程序的几个技巧》（http://sobereva.com/237）。

Q27：Multiwfn里已经载入了一个文件，怎么载入一个新文件？
A：一般建议重启Multiwfn，然后载入新文件，这样最稳妥。如果你不想重启，可以退回到程序主菜单，输入-11（是一个隐藏选项），就会看到Multiwfn刚启动的界面，然后就可以载入新文件了（这样做一般没问题。但如果之后发现分析结果异常，还是应当重启Multiwfn后再载入）。

Q28：导出的文件和图片产生到哪里了？我怎么找不到？
A：如果程序允许你指定产生文件的路径，那肯定就在那个路径下。如果提示产生在了当前目录(current folder)，那就肯定在当前目录下。什么叫当前目录，在手册最开头，以及《将文件快速载入Multiwfn程序的几个技巧》（http://sobereva.com/237）中都写明了。

Q29：Multiwfn导出的文本文件（比如绘制光谱功能导出的spectrum_curve.txt）里每一列是什么含义？
A：仔细看屏幕提示（若没看到就拉滚动条往上找），Multiwfn绝对、120%、一定会在导出文本数据的时候将文件里的每一列的含义提示得明明白白！！！

Q30：怎么通过命令行而非交互式方式运行Multiwfn？怎么把全部输出信息导出到文件里？
A：看手册5.2节，使用silent方式运行Multiwfn即可。

Q31：怎么让Multiwfn批量处理输入文件？
A：在Windows下写批处理脚本，在Linux下写shell脚本即可，非常简单。在Multiwfn手册5.3节有说明和示例。很多Multiwfn相关博文里也都利用了批处理方式运行。

Q32：Multiwfn相关博文和手册里经常提及的“实空间函数”(real space function)是什么意思？
A：实空间函数(real space function)是指自变量是体系所处的实际三维空间坐标的函数，诸如电子密度、电子密度拉普拉斯函数、静电势、ELF等等都属于此类。Multiwfn的实空间函数分析功能极强，速度很快、支持的函数种类和分析方式非常全面，能算的绝大部分实空间函数在手册2.6、2.7节都介绍了。

Q33：输出数据是一堆星号，或者显示NaN是怎么回事？
A：出现星号是由于数据太大，超过了预设的输出数据的格式所致。比如某个地方本来只能输出两位数，而实际数值是250，那么就会显示成星号了。NaN全称是not a number，也是非正常情况，比如可能是这个数据在运算过程中除以了0所致。有的时候出现星号、NaN是无害的，比如对一个阳离子做定量分子表面分析考察其分子表面上静电势特征，本来其表面上就没有静电势为负的区域，因此对静电势为负值部分计算的一些统计量可能就是这种无意义的输出，不用管它即可。但如果是本该输出有意义数据的情况却输出的是星号或者NaN，那要么是输入文件问题，要么是操作问题，要么是你对当前分析理解得有问题，要么是bug。

Q34：分析、绘制静电势的时候速度太慢怎么办？
A：仔细看《Multiwfn现已可以调用cubegen使静电势分析耗时有飞跃式的下降！》（http://sobereva.com/435），或者手册5.7节。

Q35：什么级别产生波函数适合做波函数分析？
A：波函数分析对基组的敏感性和分析方法有关。一般来说，波函数分析没必要特意用太高档次计算级别来产生波函数，因为大部分分析方法对于计算级别不是很敏感，用达到中等级别质量的波函数，比如B3LYP、M06-2X理论方法结合比如6-311G**、def-TZVP级别的基组，结果就已经足够好了，基组用到高档次3-zeta基组如def2-TZVP也就到头了。实际上，在DFT/6-31G*级别下的波函数分析结果一般也足够至少达到定性合理。因此用很高级别，比如CCSD/cc-pVQZ级别的波函数一般来说完全没必要，纯属浪费时间。理论方法一般用恰当的DFT泛函就够了，而用后HF方法产生波函数不仅很昂贵，而且一般也并不比用DFT波函数作分析有什么显著好处。

Q36：波函数分析时能带弥散函数么？
A：看你用什么分析方法。那些直接依赖于基函数的分析都不能带弥散函数，否则结果没有任何意义。另外，对于这类方法，用很大基组时的分析结果未必比用中、小基组好，比如很大的4-zeta基组结果可能还不如3-zeta基组好。这类怕弥散函数的方法有不少，比如Mulliken和SCPA分析（包括其对应的轨道成分分析、布居分析、PDOS绘制等）、Lowdin布居分析、Mulliken键级、Mayer键级、多中心键级（基于NAO的形式除外）、CDA分析等。凡是对实空间函数做的各种分析，一律都可以放心带弥散函数。如果搞不清楚的话，可以比较一下比如6-31+G*和6-31G*的差别，如果相差很大而不是一星半点，一般就说明此方法不适合用于带弥散函数的情况。众所周知，算阴离子体系的能量的时候一般都需要带弥散函数，如果你要做的分析怕弥散函数，也可以去掉弥散函数再算一次单点来产生不带弥散函数的波函数并做分析。

Q37：溶剂效应怎么在波函数分析中体现？
A：量子化学程序计算时用隐式溶剂模型即可。溶剂模型会使得溶质的波函数响应溶剂环境，因此溶质的波函数分析结果也将对应于被溶剂极化了的情况。

Q38：做某分析计算耗时高，怎么降低耗时？
A：考虑以下做法
(1)减小基组。但除非迫不得已不要低于6-31G*，否则定性正确难以保证。可以恰当使用混合基组，使得不是关键区域的原子用比关键区域更小的基组，甚至比6-31G*还小也不是不可以。
(2)简化计算模型，比如把不重要的区域直接截掉（断键处该做饱和处理的时候要恰当处理）
(3)在Multiwfn里用主功能6的选项-3或-4把不感兴趣区域的原子带的高斯型函数(GTF)删掉，这样对于之后的所有实空间函数的分析都会因此节约时间，因为Multiwfn里实空间函数都是基于GTF计算的。
(4)恰当调节设定。有些设定恰当调节的话，可以显著节约时间而不至于令结果变差。比如你通过RDG图形化考察体系某个局部区域的弱相互作用时，可以把计算的盒子范围设成仅仅框住那个区域，此时达到同样显示效果的时候，就可以比起让盒子框住整个体系的时候用更少的格点数，从而节约时间。有时也可以在精度下降可以接受的情况下通过调节某些设定来降低耗时，比如模糊空间分析模块里对各个原子空间进行积分的任务，如果把settings.ini里控制每个原子的径向和角度部分格点数的radpot和sphpot改小，耗时显然就会降低，而精度也会下降。

Q39：有些任务涉及三维空间中分布的格点，在出现的格点设定界面里应该怎么设合适？
A：Multiwfn里有很多任务是基于三维空间中均匀分布的格点来实现的，比如RDG/IGM分析、盆分析、域分析、定量分子表面分析、空穴-电子分析、(超)极化率密度分析、ICSS分析等等。计算时首先会划定一个盒子范围，这些格点会按照特定的格点间距均匀分布在这个盒子里，三个方向各有一定格点数，乘积就是总格点数。格点间距越小，分析结果就会越准确、显示的等值面会越光滑，但显然总格点数也会越高，导致耗时更高。因此设定盒子有两方面因素要考虑：
(1)格点的空间分布范围（盒子范围）：一般建议让盒子范围只框住感兴趣、被分析的区域。因为假设格点数目是固定的，盒子范围越小，盒子里的格点的间距就会越小，分析质量就会越高。如果假设格点间距是固定的，那么盒子范围越小，计算的格点数就会越少，耗时就会降低。因此只让盒子范围包围感兴趣的区域，而不让无关区域也纳入盒子范围，从哪个角度来说都是好事。怎么让盒子基本只覆盖感兴趣的区域，也确保不会有重要区域没有被纳入盒子，这需要根据你对分析方法和当前体系特征的理解来判断，没法一概而论，得具体问题具体分析。Multiwfn的设定盒子的界面里提供了很多选项用来设置盒子范围，极度灵活，比如low/medium/high quality grid是根据体系的X,Y,Z方向的边缘原子的位置往各个方向延展指定的距离来确定盒子范围的，界面里也有选项可以把两个原子间连线中点定义为盒子中心然后往各个方向延展特定距离来设置盒子，还可以直接在图形界面里可视化地挪动盒子和调节盒子尺寸等等。
(2)格点间距或格点数。格点间距直接决定分析质量，而计算耗时正比于格点数。当盒子尺寸是确定的时候，显然格点间距越小则格点数越多，反之亦然。用户应当恰当设定格点间距或格点数达到分析结果质量和耗时的权衡。Multiwfn设定格点的界面里有low/medium/high quality grid选项，对于不同功能的定义是不同的，看屏幕上的具体提示，有时对应的是总格点数，有时对应的是格点间距。对于设置的是总格点数的时候，注意low/medium/high这三个词只是对于小体系而言的，如果是很大的体系，由于盒子大了，哪怕是medium quality grid格点数的格点间距也会很大，因此实际上得到的结果是很糙的，此时得用high quality grid或者用手动输入格点间距的模式手动输入格点间距。
总之，用户应当认真理解设定格点的界面的各个选项的含义（手册3.6节里有相关说明），并根据实际情况选择适合的选项恰当地设置格点。

Q40：某些方法做布居分析、轨道成份分析时输出的诸如S、X、YZ、D0、D+1、D-1之类是什么意思？
A：这是基函数符号。S就是S型基函数，X就是X型P角动量基函数，YZ就是YZ型D角动量基函数。D0、D+1之类是D角动量的球谐型高斯函数的符号。如果你不明白什么叫球谐型和笛卡尔型高斯函数，看《谈谈5d、6d型d壳层基函数与它们在Gaussian中的标识》（http://sobereva.com/51）和《球谐型与笛卡尔型Gaussian函数的转换关系》（http://sobereva.com/97）。如果你连基组的最基础知识，诸如基函数的角动量、壳层之类都不懂，那么很难正确理解这些输出，建议看《基组入门资料小合集》（http://bbs.keinsci.com/thread-2190-1-1.html）补补基础，或者参加北京科音举办的初级量子化学培训班。

Q41：输出的结果是什么单位？
A：凡是没明确注明单位的，一律是原子单位（atomic unit，a.u.）。原子单位是一种单位制，不是一个具体的单位，对于不同的物理量的具体单位是不同的，比如对于电荷是e（e=elementary charge，基元电荷，即一个质子带的电荷量），对于距离是Bohr，对于电子密度是1/Bohr^3，对于静电势是Hartree/e，对于偶极矩是e*Bohr。如果你不清楚的话直接写a.u.就行了。原子单位的相关知识看https://en.wikipedia.org/wiki/Atomic_units。

Q42：Multiwfn给出的某种方法的分析结果为什么和其它某个程序给出的不一样，明明都是同一个输入文件？
A：可能有以下原因：
(1)其它程序对某个方法或者函数的定义与Multiwfn不同。比如NBO程序里计算Wiberg键级是以NAO为基计算的，而Multiwfn算Wiberg键级是基于对称正交化的基函数计算的。再比如AIM2000给出的电子密度拉普拉斯函数和一般定义不同，在前面多了个-1/4项。仔细看看手册就知道怎么回事。
(2)利用的输入文件里的信息不一样。比如用.fch文件作为输入文件进行分析时，Multiwfn不利用其中的密度矩阵信息（极个别功能除外），而只利用.fch里的轨道信息，但有的程序利用的是.fch里的密度矩阵做波函数分析。如果.fch文件里的轨道信息和密度矩阵信息并不是对应同一个级别的，那么Multiwfn和那个程序的结果必然不同。
(3)方法的具体实现不同。比如Multiwfn计算AIM电荷是基于均匀立方格点结合原子中心积分点算的，而AIMALL等程序里是其它实现方式。这通常不会造成定性的差异，但可能会造成可察觉的数值差异。

Q43：用Multiwfn做拓扑分析，怎么得到某个临界点上的各种函数值？
A：笔者很纳闷为什么经常有用户问这个问题，在《使用Multiwfn做拓扑分析以及计算孤对电子角度》（http://sobereva.com/108）和手册4.2节的拓扑分析的例子里都充分体现了这一点，而且拓扑分析界面里也提示的非常清楚，显然是这个选项：7 Show real space function values at specific CP or all CPs。

Q44：怎么产生cube文件？
A：cube文件是个容器格式，可以记录各种各样的实空间函数在某个空间范围内均匀分布的格点上的数值，介绍见《Gaussian型cube文件简介及读、写方法和简单应用》（http://sobereva.com/125）。所以问这个问题时你先得明确你到底要计算什么实空间函数。Multiwfn可以计算上百种实空间函数，手册2.6、2.7节都有介绍。要产生这些函数的cube文件，在载入输入文件后，进入主功能5，按照提示选择被计算的函数、设定格点即可，算完之后在后处理菜单中选2 Export data to Gaussian cube file in current folder即可导出成.cub文件。完整的例子见手册4.5.1节。

Q45：怎么考察/计算/分析电子密度？
A：这个问题非常含糊。电子密度是个三维函数，你得先明确你到底想以什么形式来研究、表征它。常见的考查方式有这些，Multiwfn都支持：
(1)计算某个点的电子密度，用主功能1实现。这有一些实际用处，比如考察键临界点位置的电子密度是AIM分析中最常涉及的手段。而考察一些芳环体系的原子核在分子平面上方比如1埃的位置的电子密度可以用来预测亲电反应位点。
(2)图形化考察电子密度在三维空间的分布。包括绘制电子密度的曲线图、平面图、等值面图，分别用主功能3、4、5实现，手册4.3、4.4、4.5节的例子看过一遍就懂了。一般来说直接对电子密度作图用处不大，因为电子密度分布是很“单调”、“乏味”的，一般在原子核位置是个极大的峰，向四周以指数型下降，这样的图上很难观察到化学上感兴趣的信息。但如果你考察的是价层电子密度，则可以讨论不少化学问题，见笔者发表的《Revealing Molecular Electronic Structure via Analysis of Valence Electron Density》（http://www.whxb.pku.edu.cn/EN/10.3866/PKU.WHXB201709252）。价层密度的绘制参考手册里4.6.2节的例子。另外值得一提的是，电子密度的0.001 a.u.等值面有特殊意义，通常被视为气相下分子的范德华表面。
(3)做布居分析(population analysis)，由此可得知各个基函数/原子轨道/原子/片段上带的电子总量，相当于在这些区域里对电子密度做积分。还可以计算原子电荷，本质上相当于原子的核电荷数减去原子带的电子数，这可以非常直观地展现实际化学环境中各个原子带的净电荷量。这些分析在文献中非常常见，也非常有实用价值，可以通过主功能7的各种选项以不同方法来计算，把手册4.7节的例子好好做一遍就理解了。没看过《原子电荷计算方法的对比》（http://www.whxb.pku.edu.cn/CN/abstract/abstract27818.shtml）一文的读者强烈建议阅读一下以了解相关基本知识。

Q46：做键级分析，有些数值很小的键级没显示怎么办？
A：那些非常小的键级是可以忽略的，如果非要获得，可以根据提示让Multiwfn导出键级矩阵文件，读取对应的非对角元即可。也可以修改settings.ini里控制键级输出阈值的bndordthres，将之设小。

Q47：Mayer键级、多中心键级怎么有时候算出来是负的？
A：首先必须确保没用弥散函数，否则结果一定没意义。如果没用弥散函数，Mayer键级有微小的负值的话，直接当成0就行了，微小负值并没有什么物理意义，是方法本身不足导致的。多中心键级也是如此。但如果算三中心键级的时候出现显著而不是微小的负值，则暗示存在三中心四电子(3c-4e)作用。可以再结合Multiwfn里的轨道定域化分析或者AdNDP分析进一步考察。

Q48：电荷分解分析（CDA）模块里绘制的轨道相互作用图里面连线非常混乱，密密麻麻，怎么办？
A：恰当设置作图参数，总能调得清楚好看。见《使用Multiwfn做电荷分解分析(CDA)、绘制轨道相互作用图》（http://sobereva.com/166）末尾的幻灯片的讲解。

Q49：我使用Multiwfn做RDG（也叫NCI）分析过程中遇到xxx问题...
A：仔细看本文，以及笔者专门写的《用Multiwfn+VMD做RDG分析时的一些要点和常见问题》（http://sobereva.com/291）。

Q50：Multiwfn做静电势的定量分子表面分析给出的极大点的数值怎么有的是负的？极小点的数值怎么有的是正的？
A：这完全没有矛盾。极大点是指这个点的数值比周围位置数值大，是相对而言的，但不代表其绝对数值非得是正的。如果体系是中性的，一般来说，数值为负的分子表面静电势极大点没有太大实际意义，可以在后处理界面里使用根据数值范围删除极值点的功能将之删掉。对于极小点也是类似的理。

Q51：怎么用Multiwfn做AIM分析？
A：AIM分析是一套理论，其中牵扯各种各样的、各种各样的分析方法，介绍看《AIM学习资料和重要文献合集》（http://bbs.keinsci.com/thread-362-1-1.html）。AIM中主要涉及的分析包括
(1)对电子密度、电子密度拉普拉斯函数、动能密度、势能密度等实空间函数绘图。AIM里涉及到的所有实空间函数都可以用Multiwfn主功能3、4、5分别绘制曲线图、平面图、等值面图来考察，分别看手册4.3、4.4、4.5节的例子。
(2)电子密度的拓扑分析，包括寻找临界点位置、考察临界点上的函数值、生成键径、产生盆间面。这可以通过Multiwfn主功能2实现。看手册4.2节的例子以及《使用Multiwfn做拓扑分析以及计算孤对电子角度》（http://sobereva.com/108）、《使用Multiwfn+VMD快速地绘制高质量AIM拓扑分析图》（http://sobereva.com/445）。
(3)对电子密度做盆分析，包括计算AIM电荷、计算原子多极矩、实空间函数积分值等。这可以通过Multiwfn主功能17实现。看手册4.17.1节的例子，以及《使用Multiwfn做电子密度、ELF、静电势、密度差等函数的盆分析》（http://sobereva.com/179）。

Q52：我已有一个格点数据文件（比如cube文件），怎么用Multiwfn计算各个原子对其中记录的函数的贡献？
A：把settings.ini里的iuserfunc设为-1，此时用户自定义函数（user-defined function）将对应于基于内存中的格点数据线性插值产生的函数。然后启动Multiwfn，载入此格点数据文件，进入模糊空间分析模块（主功能15），选择1，然后选择user-defined function，程序就会对这个函数在各个原子空间内进行积分，结果就相当于原子对这个函数在全空间内的总值的贡献量。另外，主功能15里还可以选-5来定义片段，这样可以直接得到某个片段对被积函数的贡献。这种用法的一个实际例子见《使用Multiwfn计算（超）极化率密度》（http://sobereva.com/305）的第7节。默认情况下，主功能15用的是Becke方式定义的模糊原子空间，也可以用相应选项改为比如Hirshfeld、Hirshfeld-I之类。Multiwfn也可以实现在AIM方法定义的原子盆里对函数进行积分来得到原子的贡献，但这种划分比较昂贵，化学意义也不强，这里就不多提了。

4 图像显示、绘图方面的问题

这一节第一部分是综合性问题，第二部分专门针对很多人常问的绘制平面图的功能进行解答。

4.1 综合性问题

Q53：Multiwfn的图形界面的窗口太小，怎么弄大一些？
A：从Multiwfn 3.6正式版开始，settings.ini里加入了plotwinsize3D选项，将其数值设得比默认值更大（更小）就可以加大（缩小）各个图形界面里显示三维物体的区域的尺寸，可以反复尝试选择一个对于当前运行环境最佳的值。

Q54：Multiwfn的图形界面尺寸太大，屏幕显示不下怎么办？
A：有几种做法：
(1)对于Windows，在“控制面板”-“显示”（或其它的控制操作系统的文本大小的界面）里面把文本尺寸改小，这需要重新登录系统
(2)尝试把plotwinsize3D选项数值改小点
(3)对于Windows版，如果只是主功能0的界面没法显示不完整，把settings.ini里的imodlayout设为1从而换成另一种布局再试
(4)如果是在讲课时通过投影演示Multiwfn，由于一般用的是比较低的1024*768分辨率，除非用小字号，否则窗口几乎总是显示不全。如果你不想改系统设置，可以把imodlayout设为2，此时起码对于Win7中等字号设置的情况显示效果很理想。

Q55：显示三维物体的窗口能不能通过鼠标拖动来调节视角？老是调节不到合适的角度怎么办？
A：没法通过鼠标拖动来旋转和缩放，这是Multiwfn用的图形库的限制所致。如果由于调节视角的按钮的步长太大而没法调到特别想要的视角，可以点窗口上方的Set perspective并选择相应选项，然后手动输入确切的旋转角或距离值。
另一种做法是借助免费的VMD来显示，不仅视角可以自由调节，而且图像显示质量明显更好。Multiwfn的很多分析、计算结果都可以非常容易地搞到VMD里显示出来。有些效果，如填色的等值面图，则必须通过VMD才能展现。笔者写过大量相关文章，比如《使用Multiwfn+VMD快速绘制高质量分子轨道等值面图》（http://sobereva.com/447）、《使用Multiwfn+VMD快速地绘制高质量AIM拓扑分析图》（http://sobereva.com/445）、《使用Multiwfn+VMD快速地绘制静电势着色的分子范德华表面图和分子间穿透图》（http://sobereva.com/443）、《基于Multiwfn产生的cube文件在VMD和GaussView中绘制填色等值面图的方法》（http://sobereva.com/402）、《使用Multiwfn+VMD以原子着色方式表现原子电荷、自旋布居、电荷转移、简缩福井函数》（http://sobereva.com/425）等等。

Q56：怎么设置保存出来的图像格式？
A：看手册2.8节。顺带一提，如果绘制的图像是由文字、线条构成的，建议使用pdf（或eps、wmf）格式，这样的图像是矢量图，可以无损缩放，而且线条显得非常平滑，文件也很小。默认的png格式是目前最佳的无损压缩的位图格式，适合含有复杂色彩、色彩平滑变化的图。

Q57：怎么设置保存出来的图像的像素？（有些人管这叫分辨率）
A：如手册2.8节所说，settings.ini里graph1Dsize控制曲线图的图像文件的像素，graph2Dsize控制平面图的图像文件的像素，graph3Dsize控制三维物体的图像文件的像素。

Q58：图像线条锯齿严重，怎么让图像有抗锯齿效果？
A：可以通过调节上述设置让保存出的图像的像素比较大，然后用irfanview、photoshop等程序把图像尺寸缩小。在缩小的时候，程序会通过Lanczos、B-spline等算法重新采样，之后看到的图像就没有什么锯齿了，这是一种经典的抗锯齿方式。另外，对于以线条为主的图，用pdf之类矢量格式保存，也不会看到有锯齿效果。

Q59：图像上的字体能改么？
A：改不了。如果实在觉得不好看，可以自己ps。

Q60：怎么有时刻度标签上相邻刻度的数值是相同的？比如都是0.01、0.01？
A：这是因为刻度数值的位数太少，而这些刻度数值相差又很小，导致四舍五入后看起来相同。对于曲线图，可以修改settings.ini里的numdiglinexy来增加显示的位数；对于平面图，可以修改numdigxyz。

Q61：Multiwfn保存出的图像的线条/文字太细，怎么加粗？
A：仔细看界面上的各个选项，如果界面里直接提供了设置线条粗细的选项，直接修改即可，如果改不了的话，或者是嫌文字太细，按照《加粗Multiwfn保存的图像的坐标轴和标签文字的方法》（https://www.bilibili.com/video/av26311992/）的方法通过ps加粗。

Q62：Multiwfn算出来的格点数据怎么在VMD里绘制成等值面图？
A：参考此视频的演示：《使用Multiwfn结合VMD绘制自旋密度等值面图》（https://www.bilibili.com/video/av26312131）。

Q63：观看等值面（isosurface）的时候，等值面数值（isovalue）设多大合适？
A：首先要知道，等值面是一种常用的展现三维函数在整个空间中分布特征的方式。等值面上每一个点的数值都和你设的isovalue值相同，通过等值面图的轮廓可以定性考察函数在不同空间位置的大小。isovalue的设定往往是有很强任意性的，没有唯一标准，不同isovalue下看到的等值面图像也是不同的。一般选取标准是让所得到的等值面图能较好展现不同区域函数大小的差异、能把你想主要表现的体系特征充分展现出来，同时图像美观便于理解。可以在Multiwfn里不断调节等值面数值直到满意为止。有时候可能单一isovalue下的图注定没法全面满足要求，此时可以同时给出多个isovalue下的等值面图，在极其灵活的VMD里还允许在一张图里同时显示多个等值面，比如《通过Multiwfn绘制等化学屏蔽表面(ICSS)研究芳香性》（http://sobereva.com/216）第7节的图。

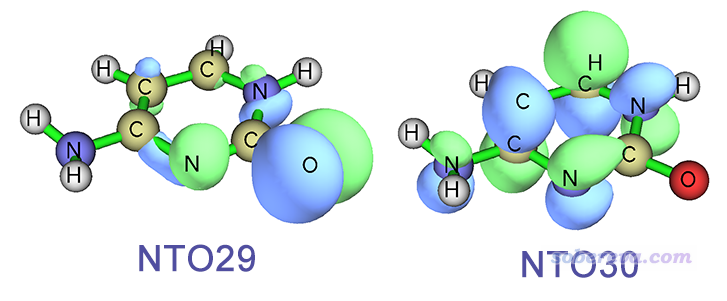
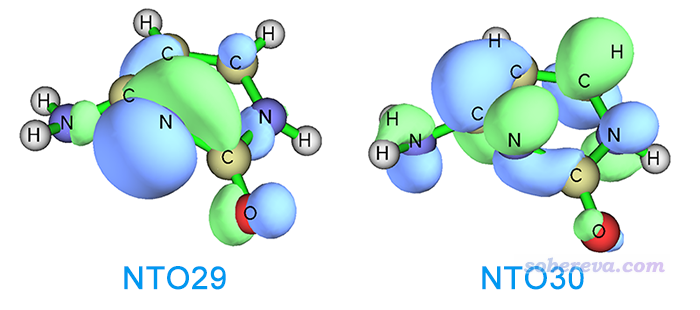
Q64：Multiwfn里显示的等值面中的绿色和蓝色代表什么？
A：绿色等值面上的每个点与你设的isovalue值相同，蓝色等值面上的每个点与你设的isovalue值符号相反。至于具体代表什么物理含义，那得看你考察的是什么函数，isovalue是怎么设的。对于专用于观看轨道等值面的主功能0，isovalue只能设为正值，因此绿色和蓝色的等值面必然分别对应的是轨道波函数的正相位和负相位的等值面。

4.2 与主功能4绘制的平面图有关的问题

笔者借此机会强烈建议打算用Multiwfn绘制平面图的用户都认真仔细照着手册4.4节一大批绘制平面图的例子操作一遍，努力领会每一步操作的含义，把这些例子都搞明白了就可以少问很多初级问题，同时掌握很多技巧。

Q65：绘制平面图时绘制体系的哪个截面合适？
A：平面图是展现三维函数在体系某个截面上的分布的方式。平面图的缺点是没法像等值面图一样把函数在整个三维空间中的分布特点通过一张图大体体现出来，但优点是可以最完整地展现某个截面上的函数变化特征。只有当你对体系某个截面上的函数变化特征感兴趣、由此可以帮助你讨论问题的时候，才适合绘制平面图来将之充分展现。比如你想通过ELF函数考察水分子中的O-H键，那就很适合绘制水分子平面的平面图，这个平面正好穿过两个O-H键键轴，因此可以很充分地体现出O-H键的内在特点。再比如，你想作图考察苯酚pi电子分布特征，那你可以在苯酚子上方比如1埃的位置，绘制平行于苯分子的电子密度的平面图（这个1埃是随意取的，差不多能大致穿过pi电子分布的主体区域）。笔者有大量博文，手册里也有大量例子，都充分体现出利用平面图可以充分讨论很多问题。如果你的体系结构特征复杂，很难恰当选取一个或几个截面充分展现体系电子结构特点怎么办？那就别绘制平面图了呗，绘制等值面图啊。

Q66：怎么设定作图区域？
A：平面图在绘制之前，需要划定一个作图区域（plotting region），即体系的某个截面上的一个确切的区域。在这个区域里均匀分布指定数目的格点，函数值就是在这些位置上计算的。在绘制平面图的过程中，你会看到Multiwfn里提供了丰富、灵活的选项来定义作图区域，各个模式在手册3.5.2节解释得非常清楚。其中有两类定义方式最为常用：
(1)绘制某个笛卡尔平面：即绘制XY或YZ或XZ平面。假设你选的是绘制YZ平面，由于YZ平面有无数个，每个对应不同的X值，因此程序还会让你输入X值。程序会根据体系Y和Z坐标最大、最小的原子的位置划定实际作图区域，并往四周延展指定距离（称为“extension distance”，延展距离），免得绘制出的图的边缘正好卡着边缘原子的原子核位置，造成感兴趣的区域被截断。
(2)通过三个点定义一个平面：中学都学过，三点定义一个面。你可以手动输入三个点的坐标，也可以通过输入三个原子序号通过它们的原子核位置来定义一个面。实际的作图区域按照下图示意的方式来确定

上图中，extension就是延展距离，X和Y轴就是绘制出的图像的横轴和纵轴，实际的作图区域是蓝色虚线框住的范围。可见，三个点（或原子）的选择，以及三个点（或原子）输入的顺序，不仅影响作图区域的大小，也影响图像的朝向。用户应当根据实际情况恰当设定以得到满意的结果。

Q67：感兴趣的区域在图上显示不全怎么办？
A：作图区域是怎么确定的，在上面已经解释得很清楚了。显然，加大延展距离就可以让作图区域变得更大，让原本没显示出来的地方也可以被纳入到作图区域中。设定延展距离的选项就是定义作图区域那一步里的选项0: Set extension distance for plane type 1~5。当你通过三个点（或原子）定义作图平面时，如果选择的点很不合理，那么即便加大延展距离也不会有好的效果，可能导致真正感兴趣的区域又歪斜又严重偏离中心位置。

Q68：绘制出来的平面图里面的内容是歪着的，或者感兴趣的区域不在图像的中央，怎么解决？
A：一种做法是在定义作图平面的时候恰当定义，结合上文的示意图，恰当选择三个原子或者输入三个恰当的点。还一种做法是先尝试绘制一次，记录下歪斜的角度和偏离中心的程度，然后在重新绘制的时候在定义作图平面时设定旋转角和平移量，详见此贴的示例：http://bbs.keinsci.com/thread-11037-1-1.html。如果你并不需要坐标轴的话，最简单的方法是通过ps等程序直接把图像中需要的部分抠出来，然后旋转一下就完了。

Q69：绘制的平面图里面有些原子的标签没显示出来是怎么回事？
A：只有当某个原子与作图平面的垂直距离小于特定阈值时，这个原子在这个平面上的投影位置才会显示出原子标签（倘若没有这个阈值设置，所有原子标签都显示出来，对于大体系，图上的标签将何等混乱可想而知）。没显示出来标签的那些原子显然是因为其距离作图平面超过了默认阈值。阈值可以在后处理界面通过选项17 Set the distance criterion for showing atom labels进行修改。阈值设定之后，你还可以选择是否把超过这个阈值的原子用比较细的字体显示出表现，以区别那些离作图平面比较近的原子。

Q70：等值线图里面怎么标注等值线数值？标注的数值不好看怎么办？
A：后处理菜单中选2 Enable showing isovalue on contour lines然后重新作图。程序自动会在曲率比较小的线条上标注等值线数值，可能标的位置不太合期望，而且可能有人嫌字号、字体不理想，这没办法，毕竟计算机程序没有人的审美。你可以参考着自动标注的等值线数值，自行用ps之类工具把等值线数值以你觉得最美观的方式标上去，比如笔者J.Mol.Model.,19,5387(2013)这篇文章里的图3就是这么做的。

Q71：等值线图怎么设置等值线数值和线条颜色、粗细、风格？
A：用后处理菜单中的选择3 Change setting of contour lines进入等值线设定界面，其中各个选项的含义一看选项上的文字就能秒懂，在手册3.5.4节还有详细解释。线条粗细和风格可能在屏幕上直接显示的时候体现不出来，但在保存的图像中肯定会体现出来。

Q72：怎么在填色图上把等值线也同时显示上去？
A：照常绘制填色图，然后在后处理菜单中把显示等值线的选项打开。

Q73：平面图里的横、纵坐标单位怎么改为埃？
A：后处理菜单里选择-8 Change length unit of the graph to Angstrom。

Q74：填色图里为什么有的区域是白色、黑色的，代表什么？
A：白色代表函数数值高于色彩刻度上限的区域，黑色代表低于色彩刻度下限的区域。如果你把settings.ini里的inowhiteblack设为1，则高于上限和低于下限的区域会分别用上限颜色（红色）和下限颜色（深紫色）展现。

Q75：填色图、着色等值面图的色彩刻度上下限怎么设合适？
A：一般来说，色彩刻度（color scale）的上下限的设定的主要原则是能够通过色彩的不同，使得图中不同区域函数值的差异能充分展现出来，而且从审美上比较漂亮。色彩刻度范围若设得太宽，不同区域的颜色差异往往体现得不够显著；刻度范围若设得太窄，函数值超过刻度范围的区域就完全没法体现出差异。因此刻度范围必须择情而定，需要反复尝试找到尽可能理想的。

Q76：填色图里色彩刻度的颜色过渡方式能改么？
A：改不了。如果你想用别的色彩过渡方式，比如“蓝-白-红”之类，得让Multiwfn导出平面图的文本数据为plane.txt，然后载入sigmaplot、surfer、Origin、matlab等程序再绘制填色图，届时作图设定更丰富，可以改色彩过渡方式。

Q77：我把平面图的平面数据导出成plane.txt之后，想用sigmaplot之类的第三方程序绘制，用哪几列数据绘制？
A：导出文件的时候仔细看屏幕上的提示，根据实际情况判断。比如你绘制的是YZ平面，程序会提示The column 1,2,3,4 correspond to X,Y,Z and function value, respectively，显然在第三方程序里绘制时，横轴和纵轴分别应当用第2、3列的数据，而函数值对应第4列。
再比如你通过三个原子定义作图平面，导出数据时Multiwfn会提示你
The column 1,2,3 correspond to Cartesian X,Y,Z coordinates, respectively
The column 4,5,6 correspond to X,Y coordinates in the graph and function value, respectively
显然，应该将4、5、6列的数据分别作为横轴、纵轴和函数值，而对应于格点在实际三维空间中的X,Y,Z坐标的1、2、3列当前用不着。

Q78：填色图的色彩刻度条的标签间隔怎么改？
A：后处理界面里有选项-2 Set stepsize in X,Y,Z axes进行设置，其中的Z轴就是指色彩刻度轴。

Q79：图上的原子标签能改成显示原子序号么？字号、字体能改么？
A：后处理菜单中选择18 Change style of atomic labels可以修改显示方式，可以选择只显示序号、只显示元素、元素和序号同时显示，默认设置可以通过settings.ini里的iatmlabtype来设。标签字号可以通过settings.ini里的pleatmlabsize来设。字体改不了。

Q80：绘制出来的平面图怎么和分子结构图合并到一起便于观看？
A：看《将分子结构图和Multiwfn绘制的平面图准确合并的方法》（http://sobereva.com/274）。另外，Multiwfn在后处理界面也提供了选项8 Enable showing bonds可以将化学键（根据距离判断）用直线显示出来，这样也可以使得体系结构在平面图上体现得更清楚。

Q81：平面图的横、纵坐标对应什么？
A：当你绘制的是某个笛卡尔平面时，比如你当前选的是YZ平面，那么图上的横轴、纵轴坐标就分别是平面图上数据点在三维空间中的Y、Z轴坐标。如果你是通过其它方式定义的作图平面，那么横、纵坐标仅仅体现的是距离作图平面起点位置的相对坐标，只反映相对空间关系，和三维空间中的X,Y,Z坐标没有直接联系。

Q82：怎么把AIM分析中的临界点、键径、盆之间的分界面显示在平面图上？
A：先用主功能2做AIM拓扑分析，然后退回主菜单，再照常绘制平面图，凡是于作图平面距离小于阈值的临界点、键径都会直接显示在图上。而且在后处理菜单中有选项可以在图上生成和绘制盆之间的分界面。详见手册4.4.6节的例子。

Q83：怎么用Multiwfn基于格点数据文件绘制曲线图、平面图？
A：把settings.ini里的iuserfunc设为-1，此时用户自定义函数（user-defined function）将对应于基于内存中的格点数据线性插值产生的函数。然后启动Multiwfn，载入此格点数据文件，进入绘制曲线图或平面图的功能（主功能3、4），被绘制的函数选择user-defined function即可。

↧

使用CYLview绘制高质量分子结构图和制作化学反应演示动画（视频演示）

December 25, 2018, 4:26 pm

≫ Next: 在VMware 15中安装CentOS 7.6的完整过程视频演示

≪ Previous: Multiwfn FAQ

使用CYLview绘制高质量分子结构图和制作化学反应演示动画

文/Sobereva@北京科音 2018-Dec-26

CYLview的虽然功能不算多强大，但它在作图的很多特性方面没有其它程序能很好取代，所以笔者特意录制了长为11分钟的使用CYLview绘制分子结构图和制作各种类型动画的演示视频，见：https://www.bilibili.com/video/av39041185

本文内容是对视频内容进行一些补充说明。视频里并没有把CYLview所有特性一一展现，而是着重把新用户容易犯懵，不是显而易见，不容易自己试出来的操作进行了讲解，很容易理解的操作和选项视频里就没有去提，用户自己把玩几分钟就会得差不多了。

CYLview的下载地址是http://www.cylview.org。视频里用的版本是CYLview 1.0b Build 561。

如果机子里没装化学文件格式转换程序Openbabel的话，CYLview只能载入Gaussian输出文件，因此很不方便。所以强烈建议在机子里装上Openbabel，是个免费程序，在此文里有简单介绍：《基于OpenBabel批量产生特定基团以任意方式接到苯上的结构的方法》（http://sobereva.com/440）。

有些人发现目前的CYLview载入不了G16的输出文件，是因为没有按照视频里提及的方式去点击更新程序按钮，更新过之后就没问题了。

视频里使用了Houkmol的style，这是CYLview里内置的一种显示风格的组合，是搞有机体系计算知名的Houk文章里常见的显示风格。

视频里的renderall.bat是个DOS批处理文件，内容如下
for /f %%i in ('dir *.pov /b') do (
povray +W640 +H480 +A %%i
)
将这些内容复制到一个文本文件里，改名成renderall.bat即可使用。此脚本会调用当前目录下的povray.exe对当前目录下的所有povray渲染器文件（.pov）进行渲染，产生出同名图像文件。

视频中用的ffmpeg是业界非常知名的视频编码、解码、转换程序，免费，小巧，功能极强，支持格式众多，各个操作系统都有，可以在https://ffmpeg.org免费下载，Windows版解压即用无需安装。基本使用格式为ffmpeg [选项] [输入选项] -i [输入文件] [输出选项] [输出文件]。

制作mp4动画时用到了以下命令
ffmpeg -r 15 -i FRAME%04d.png -crf 22 video.mp4
其中%04d代表通配0001、0002、0003...。-r后面是每秒的帧数，视频实际长度就是图像数目除以r值，因此r越大动画播放越快，r越小播放越慢。-crf是ffmpeg调用的名为x264的编码器里的参数，数值越小动画越清晰，但是文件越大，一般-crf 22就比较合适。

制作gif动画时用到了以下命令
ffmpeg -i FRAME0001.png -vf palettegen palette.png
ffmpeg -r 15 -i FRAME%04d.png -i palette.png -lavfi paletteuse video.gif
虽然ffmpeg也可以一步就产生gif动画，即把前述命令的mp4后缀改成gif，但是动画里的某些颜色比较诡异，远不如上面这样先根据实际图像文件生成调色板文件，再产生gif动画来得好。gif文件比mp4大得多，而且只能包含256色，但好处是可以直接嵌入到网页和ppt里。

视频里笔者写的用于合并带_txt后缀和不带这个后缀的.pov文件的CYL_mergeTXT.exe工具在这里下载：http://sobereva.com/attach/453/CYL_mergeTXT.rar。带_txt后缀的文件只包含标签内容，而不带这个后缀的包含的是分子结构信息。

视频里用的将GauIRC2xyz在这里下载：《将Gaussian的IRC任务输出转换为.xyz轨迹文件的工具》（http://sobereva.com/285）。

笔者还写过其它与制作计算化学相关视频有关的文章，如下所示，里面用的imagemagick工具也都可以改用ffmpeg工具，速度更快而且还有Windows版。
制作动画分析电子结构特征
http://sobereva.com/86
通过键级曲线和ELF/LOL/RDG等值面动画研究化学反应过程
http://sobereva.com/200

↧

在VMware 15中安装CentOS 7.6的完整过程视频演示

December 31, 2018, 1:08 pm

≫ Next: VASP最简单的安装方法（含全程视频演示）

≪ Previous: 使用CYLview绘制高质量分子结构图和制作化学反应演示动画（视频演示）

视频地址：https://www.bilibili.com/video/av39555524/

因为给别人解释怎么安装计算化学程序的时候，对方有极大概率是Linux零基础，不知道系统怎么装，或者装了也是瞎装，故录此视频。完全Linux零基础的人严格照着此视频也可以顺利安装最适合计算化学工作者使用的CentOS。本视频虽然用的是VMware装的，但对于实体计算机，只要把镜像烧到U盘或光盘并由其启动，之后的安装过程和视频里完全一样，只不过应在安装界面里根据实际情况对硬盘进行分区。笔者介绍、演示的很多计算化学程序的安装时，所用的系统都是按照此视频里的方式安装的。

顺带一提，VMware虚拟机对运算性能的损失一般不超过10%，如果计算机不是只跑Linux计算程序用，那么在Windows下运行日常应用程序，而用VMware跑Linux的程序是很合适的（这里不对Win10 WSL做任何讨论，好用Win10 WSL者可以忽略此视频）。

↧

VASP最简单的安装方法（含全程视频演示）

December 31, 2018, 9:35 pm

≫ Next: 2018年下半年观看的非TV版动画简评

≪ Previous: 在VMware 15中安装CentOS 7.6的完整过程视频演示

VASP的最简单的安装方法

文/Sobereva@北京科音 2019-Jan-1

目前计算化学公社论坛（http://bbs.keinsci.com）上的第一性原理板块里已经有多篇写得很好的关于VASP的编译方法的帖子了。笔者这里写一个初学者最易于理解的版本，不仅所需要的操作步骤是最少的，而且编译出来的VASP运行效率几乎是最高的。考虑到少数读者可能存在阅读理解能力障碍、极其不情愿看文字，本文的安装过程笔者录了完整的演示视频，见https://www.bilibili.com/video/av39616222/。我相信，哪怕是对Linux、VASP、编程零基础的读者，只要严格模仿演示视频，也一定可以非常顺利地安装。也希望这些零基础VASP用户看了此视频后不会再去花钱找人装VASP或者花钱买网上乱七八糟的VASP安装视频。

本文用的软件版本和系统都是撰文时的最新版。编译的是VASP 5.4.4，操作系统是CentOS 7.6，编译器和MPI/MKL库是Intel Parallel Studio XE 2019 Update 1，其中的ifort编译器就是19.0.1版。Intel编译器目前不是免费的，但可以获取试用版。CentOS是在笔者来看最适合计算化学研究者使用的Linux操作系统，免费、稳定、设计合理、用户规模庞大、兼容性好、安装各种计算化学程序省心，不仅是最流行的计算服务器用的操作系统，初学者使用起来也没任何压力。本文安装过程用的账户是root账户，如果你用的是普通用户，本文中的安装路径需要做相应的调整。如果读者用的系统、程序、编译器版本和此文的不同，也有极大可能无法按照此文的方法安装，请随机应变。另外，使用较新系统、程序版本的读者，不要再去参考网上众多年代较早的编译VASP的文章，要么编译过程繁琐，要么根本不适合当前情况。

如果读者不会装CentOS系统，或者之前装过但是是瞎装的，强烈建议严格效仿此视频里的方式安装：《在VMware 15中安装CentOS 7.6的完整过程视频演示》（http://sobereva.com/454），可以很容易地装好系统，而且之后编译安装各种计算化学程序也都会比较顺利。

1 安装Intel编译器和相关的库

将parallel_studio_xe_2019_update1_cluster_edition.tgz包拷贝到Linux里面，通过tar -xzf [文件名]将之解压。如果当前处于图形环境，就进入此目录，在命令行下运行./install_GUI.sh启动Intel Parallel Studio XE的图形界面的安装程序。如果你是在纯文本环境下，就运行./install.sh启动文本界面的安装程序，但是在自定义组件的时候操作比较繁琐。

对于root用户，默认的安装路径是/opt/intel，这里就用默认路径。如果你想省硬盘，安装过程中可以选择自定义，对于编译计算化学程序完全用不着的组件都可以不去装。其中IA32版的组件都不装，因为我们编译程序都是编译64bit版本。要装的组件里只有以下这些是必须的
·Intel Fortran Compiler
·Intel C++ Compiler
·Intel Math Kernel Library 2019 Update 1 for Fortran里的Intel MKL core libraries for Fortran、Fortran 95 interfaces for BLAS and LAPACK、Cluster support for Fortran
·Intel Math Kernel Library 2019 Update 1 for C/C++里的Intel MKL core libraries for C/C++、Cluster support for C/C++
·Intel MPI Library 2019 Update 1里的Intel MPI Library for applications...
·Intel Threading Building Blocks 2019（这是Intel C++ Compiler必须依赖的）
安装时可能会显示缺少32bit库之类，不用管，继续装即可。

装好后，使用比如gedit ~/.bashrc命令编辑当前用户目录下的.bashrc文件，这里面的内容是每次进入bash终端时自动运行的。把下面这行加入其中末尾，用来自动配置Intel Parallel Studio XE的运行环境
source /opt/intel/parallel_studio_xe_2019/psxevars.sh
（如果你之前装了其它MPI库，应当把.bashrc里相应配置在开头加上#注释掉，免得造成冲突）
然后重新进入终端，运行ifort -V，如果显示出了编译器的版本，说明编译器已经可以正常使用了。

然后进入/opt/intel/compilers_and_libraries_2019.1.144/linux/mkl/interfaces/fftw3xf，运行make libintel64命令，过一会儿当前目录下会产生libfftw3xf_intel.a库文件。

2 编译VASP

解压VASP包，得到vasp.5.4.4目录。进入此目录，把arch/makefile.include.linux_intel拷到上一级目录下改名为makefile.include，里面的配置专门适合Intel编译器。打开此文件，把其中的OFLAG参数里加入-xhost，这样编译器会使得编译出的程序能够利用当前机子CPU能支持的最高档次的指令集以加速计算，也因此就没必要手动添加其它一些VASP编译教程里诸如-xAVX、-mSSE4.2之类的选项了。

之后运行make all命令开始编译。一般半个小时到一个小时可以编译完毕。

编译完成后，在vasp.5.4.4/bin目录下出现了vasp_gam、vasp_ncl、vasp_std三个可执行文件，分别是Gamma only版，非共线版和标准版。为了使用方便，可以把最常用的vasp_std改名为vasp。然后在~/.bashrc末尾加入以下这行，使得此目录加入到操作系统寻找可执行文件的路径中：
export PATH=$PATH:/sob/vasp.5.4.4/bin
之后重新进入终端，VASP就可以用了。

3 测试VASP

下载测试任务包http://sobereva.com/attach/455/benchmark.Hg.tar.gz，这是个含50个Hg原子的标准测试任务。将之解压，会看到IN-short和IN-long，分别是一个耗时较短和一个耗时较长任务的INCAR文件。这里将IN-short改名为INCAR，进入此目录，输入mpirun -np 4 vasp测试调用四个核心执行此任务，然后检查得到的OUTCAR看是否内容正常，没异常的话就说明完全装好了！

↧

2018年下半年观看的非TV版动画简评

January 1, 2019, 2:48 am

≫ Next: GROMACS的安装方法（含全程视频演示）

≪ Previous: VASP最简单的安装方法（含全程视频演示）

2018年下半年观看的非TV版动画简评

文/Sobereva 2019-Jan-1

以前Sobereva只写观看了的TV版动画评论，但是我看的OVA、OAD、SP、剧场版等额外形式的动画也不少，不写评论可惜了，因此这里对从2018年9月15日开始截止到2018年12月31日观看的非TV版动画也都进行简单评论，以后也会一直写此类评论。还有些此类动画看完后忘写了，就也不再补了。由于这类动画不好对比和打分，我也就不给出评分了。

牵牛花与加赖同学
类型：剧场版
长度：58m
这真是一部非常好的百合动画，喜爱百合作的人绝对不能错过此作，又有趣又有爱。此作对人物内心刻画细腻，场景表现力很强，充分地刻画出百合最美的一面。观看过程中就觉得俩女主山田和加濑这俩人真般配，非常有缘分，特别是看到最后，感觉她们之间实在太有爱了，绝对不能拆散。对这俩人来说，彼此都是“非她不可”。ED歌曲超级好听，看了此作令人感动的结局，再一听ED，感觉内心被爱填满了。ED的歌词也真棒，非常抒情和打动人心。加濑看起来有点男孩子的感觉，个子高高的，作风大大咧咧，坐在墙根的时候都是敞着腿，而山田则是典型的清纯内向的少女，光从设定上看这种组合就挺容易走到一起的。加濑刚到山田家，就想着和她发生肉体接触，而且光是接吻都还嫌不够，从这种生理方面上，感觉加濑也挺像男孩子（笑）。加濑看起来广交朋友，外人看起来好像和谁都能搞在一起，但山田在加濑心中却有着非常特殊的位置，无可取代，很多场景中，从加濑对山田说话的语气上就能看出加濑对山田是多么的重视。加濑过于闪耀，每天都被各种朋友簇拥着，就像向日葵一样，而山田则显得平淡无奇，总是一个人独自默默地打理花园，这样大的反差令山田有一种不安全感，觉得自己对加濑而言只是一时的邂逅，最终她肯定会走向更远的地方而离开自己的视线。好在山田最终下了决心，奔向即将远去的加濑，做了可能是她这一辈子最出格的一件事。山田此时能拥有这份勇气，既证明加濑是她真心无法割舍的，也证明自己是加濑命中注定的人。加濑是佐仓绫音配音的，众所周知佐仓是个多么痴的CV，佐仓在此作中真是本色出演，她自己肯定感觉很high。

紫罗兰永恒花园 Extra Episode
类型：OVA
长度：34m
当时看紫罗兰永恒花园TV版，被此作深深打动，给出了97的超高分，而此作的这个OVA，看罢再次令我赞叹不绝，又一次深感天朝动画要追上日本还得有几十年才有可能。这OVA质量实在非常高，处处做到了极致，看完之后我都鼓了好几下掌，再次给京阿姨跪了。这OVA的剧情是violet接受委托，给一个唱歌剧的女人代笔写情书，但那情书内容实则是要被用于为了抚平战争创伤而创作的新歌剧的歌词。violet被反复刁难，好在最后由于机缘，看到了战争期间对上前线的亲人、恋人们所写的饱含思念的文字，回想起了自己对少佐的心意，最终创作出了“令所有女人都共鸣、令所有男人都感动”歌词，与此同时自己距离对“爱”的真正认识更加深了一步。看这个OVA再次感觉violet实在太美了。此作里唱歌剧的人演唱功力也真是厉害，感染力特别强。当初给violet上自动人偶课的那个老太太真是有眼光，没想到她能敏锐地捕捉到violet的杰出潜力，因而唯独推荐violet来做这个超级艰难的任务。

黑子的篮球Last Game
类型：剧场版
长度：1h30m
我一直很喜欢《黑子的篮球》，在我心目中的位置并不比灌篮高手低。这个剧场版令我极度满意，制作非常精良，诚意满满，从头到尾无尿点，用“酣畅淋漓”这个词来形容此作是最适合的。这剧场版内容是奇迹的世代五个人和黑子、火神聚集到一起组成日本最强队伍，和一个世界最强、特别拽、傲慢无礼、侮辱日本人的街球篮球队打一场篮球的事。此作的90分钟里大部分时间都是讲这场比赛的过程，场面惊心动魄，一个接一个开挂，一挂比一挂高，局势跌宕起伏扣人心弦，令人难以预料。中途虽然插有回忆杀但是不多，因此没有破坏比赛连贯性。之前看黑子的篮球TV版最气的就是，看到正high的时候，一话就结束了，而这个剧场版看得可谓一本满足，爽到飞起，精彩万分。尤其是最后双人开zone大力扣杀终于险胜，那一刻感觉像身体高潮了一样。说实话，感觉青峰的表现没有达到我的预期，我当初心目中最强的就是青峰，但感觉这次比赛中没有表现出近乎无敌的感觉，甚至1v1对付对方的那个各方面数值都爆表的大块头的时候还吃亏。最后火神和黑子在机场那一段真是非常基情，这俩真是命中注定的CP。这个剧场版做得真心特别好，遗憾的是虽然引入了国内，但引入得太晚了，电影院上映前N天我就已经下载了熟肉（虽然一直压着没看），导致票房惨淡。而且电影院排的场次也少，本来打算第二天去电影院看，居然那天发现已经下映了。引进方应该好好自我检讨。

舰娘剧场版
类型：剧场版
长度：1h33m
我对舰娘系列挺喜欢的，TV版做得不错，但这个剧场版感觉很一般，看完之后没什么触动，而且前一半很沉闷。这次女主还是吹雪，要是换个高人气的舰娘当女主多好。这次的异变的源头是吹雪在挂掉之后分离出的消极绝望情绪的化身。我很喜欢的大和在TV版没有太多表现，而剧场版里还算是出镜挺多，表现出了强大战斗力和大姐姐似的可靠感。TV版如月被突然干掉，令人很伤心，这回一开始如月回来了，我还挺高兴，没想到最后又虐如月一遍，唉，不过最后一幕如月不知道怎么又活了，感觉有点强行happy end。我酷爱的岛风在此作完全是打酱油，露了个屁股就没再出现，令我感到十分不满。希望舰娘能出TV动画第二季，强烈呼吁女主改为岛风或天津风。

向山进发第二季 OVA
类型：OVA
长度：16min
这个OVA还挺有趣的，是综艺节目风格，内容是经典场面回放，但并不是简单的总集篇，而是把之前的一些故事片段原场面后面加上新创作的一些夸张和无厘头内容。感觉日向穿西装还挺有范儿的，比她穿女装更合适，而且她和葵的“男女搭配”感觉非常协调。

中二病也要谈恋爱-Take On Me-
类型：剧场版
长度：1h33m
这是TV版剧情的后续，之前勇太和六花互相表露了心意之后，迟迟没有进一步发展，而六花的姐姐十花又强行要把六花带到国外生活，于是二人就私奔了。此作主要剧情就是二人躲避姐姐的追捕，一路私奔，最后见到六花的母亲的过程。期间六花一直对男主放不开，后来才真相大白，六花非常珍惜和重视男主对她的感情，也想永远和他在一起，但自己却总觉得，当她和男人结合后，自己一直维持的设定将崩溃，将陨落人间，而这样的她将不是勇太所喜欢的。其实六花完全想多了，勇太对她的深切的感情绝不仅仅是因为她是中二设定这么简单，而六花就算和男主结合，我觉得这与中二设定其实也没有什么矛盾的，一辈子中二也没什么嘛，她的自我烦恼完全是多余的。好在最后解开了心结，全身心接受了男主。中二病的故事应该算是到此彻底结束了，是非常圆满的happy end，十花也放下了对六花未来的顾虑，将她托付给了勇太。六花她妈第一次在动画里出场，我感觉六花她妈很漂亮，而且性格和十花完全相反，十花非常强势，而六花她妈却很温柔内敛。想不到最后十花这样的御姐居然结婚了，还以为没有人能驯服她这样的女强人。我当年是很推森凸CP的，不过时间长了，已经有点淡忘了，不过看了这个剧场版，感觉一本满足！这个剧场版看得我最happy的地方就是二人的互动，虽然总互相掐架，但是却同床共枕，真是美好得不得了，而且十花在手机里保留了二人意外接吻的瞬间，真是GJ！我觉得，就算此作故事还有什么后续情节，森凸这对CP也是板上钉钉了，不再可能有任何岔子了。

品酒要在成为夫妻后 14话
类型：OVA
长度：3min
想不到TV版结束后那么久竟然出了个OVA。女主的欧派真大啊，洗澡时候眼福眼福，诱人诱人。令我挺意外的是明明都是夫妻了，居然女主洗澡时候还怕男主看到她果体，真是怪哉！

反叛的鲁路修3：皇道
类型：剧场版
长度：2h20min
没想到隔了那么久突然来了个剧场版。当初鲁路修是10年前看的，我评价极高。这个剧场版就是把之前TV版后期的故事再整合到一起重新制作一遍。制作质量真是相当精良，唤醒了我当年的记忆。虽然剧情都早就知道了，但还是再次感叹鲁路修真是一个伟大、非常了不起的人。TV版结局是CC和鲁路修都去了农村隐居起来，鲁路修驾驶着马车那一幕我还印象很深刻，但是这个剧场版最后就只有CC在乡下的镜头了。剧场版末尾来了个悬念，难道之后还要出新作，让鲁路修复活？（貌似是这样，已经有风声了）

幽游白书 BDBOX 新OVA
类型：OVA
长度：29min
此作来了个OVA真是很突然，少时对幽游白书还是挺喜欢的。看到当年记忆中的角色在这部OVA里再次出现，真是很欣慰的事情。这个OVA算是原作里早期故事中的一个插曲，藏马还是短头发。B站上还有幽游白书TV版的完整动画，曾经还入迷，一口气看了好多，后来想想要是都看完的话不知得荒废多少时间，就作罢了。

少女☆歌剧 Revue Starlight OVA 01,02
类型：OVA
长度：7min
OVA 1：
内容是讲此作的少女们在更衣室量胸围的故事，这故事显然很有趣味和看头。大场奈奈和双叶体格和欧派的对比真是超级悬殊，之前都没注意到双叶如此又矮又平。后来神乐光管闲事想开导双叶，和双叶借此搞好了关系，还挺有意思。
OVA 2:
讲神乐光与天堂真矢在楼梯相遇，真矢嫌光演的不理想，而光怼了回去，光表达了自己对角色的认识，令真矢心服口服。没想到真矢也会示弱，因为不甘被比下去而释放自我大声叫喊那一段很搞笑，颠覆了我对她的印象，我以为真矢是那种因为No.1而完全高傲的存在，万万没想到真矢其实也有弱者通常具有的想法，只不过从来没机会表现出来。真矢X光这个邪教感觉也可以有。

在离别之朝竖起约定之花
类型：剧场版
长度：1h54min
此作的画面超级惊艳，刚开场时候，那画面质量我看得都惊了，很多场面非常唯美，有的就像专业摄影师的杰作。且不说别的，光这画面就足够值得看的。好多场景我都截了图当桌面了，此作一定要看>=1080p的版本。此作音乐也绝赞！有的婉转动人，有的气势恢宏，把此作表现力和意境拉到更高的高度。此作的ED也简直美哭，歌声太轻盈细腻了，再加上ED精心制作的织布的特写图，真是极致的美的享受，我不禁跟着歌词唱起来。此作也不是光靠卖画面和音乐，把此作完整看完，感觉剧情也不错，最后很感人。此作主要内容是有有一群伊欧夫人一直隐藏在不为人知的地方年复一年日复一日地织布，他们不老不死，但后来邪恶的人类君主想让伊欧夫女性给他生孩子，使自己后代获得永生，于是派兵入侵之将之并灭族。其中女主玛奇亚逃了出来，中途捡了个叫艾瑞尔的婴儿，之后作为他的母亲，拼尽全力，悉心抚养他长大。整部作品主要情节就是描写艾瑞尔的成长过程，并着重刻画他与玛奇亚关系的变化。玛奇亚作为伊欧夫人，身心永远保持者15岁的少女状态，但是艾瑞尔却不断长大，从婴儿变成幼儿，幼儿变成儿童，儿童变成少年，少年变成青年，再到历经几十年后，变成垂暮的老人。一路看下去，最后依然年轻的玛奇亚握着在床上安息的苍老的艾瑞尔的那个场景真是太催泪了。我在这一刻，真是特别感觉到岁月的无情，也深刻感受到了，为什么很多作品里那些不老不死的角色，那么希望一死。他们看到自己珍视、深爱的人一个一个因苍老而去世，而自己却不能陪伴他们远行，怎能不极度感伤？从外貌和心智来看，最初玛奇亚和艾瑞尔之间完全是母亲和孩子的角色，艾瑞尔完全依赖于自己的妈妈。但很快，艾瑞尔就长大了，看起来和自己的母亲已经是相同年纪的少年了，这时候，玛奇亚这个“妈妈”似乎已经不再是“妈妈”了，甚至他对“妈妈”还起了男女之间的感情。如此“合理”的与名义上的母亲发生恋情，感觉有一种极其微妙的禁断的感觉，我心里此刻憋着有好多槽要吐，但不知怎么吐才能彻底吐痛快。不过艾瑞尔终究和玛奇亚没有交往，要不然“妈妈”和“儿子”结婚、生子，虽然只是名义上的母子关系，但在伦理上也实在显得太背德了。没想到艾瑞尔后来是和别的姑娘结婚了，不过我想艾瑞尔终究还是对她的“母亲”玛奇亚有超越母亲的感情，但他却不能表达。此作的脚本和监督都是冈妈，感觉冈妈这剧情真是“有水平”！弓虽！

工作细胞：Special 感冒综合征
类型：OVA
长度：23min25s
这一话播出的时候差不多圣诞节，感觉有点像年末的大礼。这一话制作一如既往地好，而且感冒病菌入侵方式很有新意，不正面冲突，而是同化机体细胞，试图从内部瓦解机体。香菜这一话完全是打酱油。八云紫style的巨噬细胞在这一话里表现得挺美。希望这样的OVA多出一些。

游戏3人娘(来玩游戏吧) OVA 01 02
类型：OVA
长度：2*6min57s
这两话挺有趣的，比正片多数内容都更有趣。第一话讲玩弹球和调戏小正太弟弟，第二话讲掰腕子。到底还是没弄清楚那个曾经与巨乳女主邂逅的人是伪娘还是真娘。

游戏3人娘(来玩游戏吧) 01
类型：OAD
长度：13min21s
这一话里EVA那个梗相当有趣。后一半讲述女老师年轻时候的故事，这个剧情挺有意思，如果此作后续作品里多介绍介绍那个老师当年的往事就好了，她那两个女同学都比她颜值高很多。最好此作之后也讲讲老师的恋爱经历，我对此挺感兴趣。

齐木楠雄的灾难完结篇 01 02
长度：2* 23min39s
没想到时隔那么久突然来了个完结篇，这两话依然很有趣，齐木终于压制住了火山爆发，不需要再重新loop高中生活了。虽然出了这么两话挺惊喜，但看到“完结篇”这三个字同时又感到有点遗憾，而且第2话确实像是happy end。但愿以后还能再出续作。照桥对齐木的喜欢程度感觉比以前又高了，这俩人若不能在一起就太可惜了。

在12月上旬去大阪采风期间，在Toho cinema电影院看了以下三部动画

ANEMONE/交响诗篇艾蕾卡7 Hi-evolution
类型：剧场版
听说过交响诗篇系列，但是没看过前作。在电影院看到有动画作品正在上映，就看了。此作剧情看得一知半解。有的地方感觉和EVA有那么点相似。整部作品一会儿战斗一会儿说话。战斗部分制作质量相当高，尤其是最后与BOSS战斗的部分，水准非凡。最后此作女主进入另一个世界，把那里面的一个绿毛妹子强行带出那个世界，那一幕制作得挺有震撼力的，无数老鼠似的东西疯狂以物理效果方式疯狂往这个空间里涌现，画面和音乐结合在一起令人感到万分惊险刺激。这俩妹子之间令我嗅到了百合的味道。

怪兽娘黑
类型：剧场版
我之前只是听说过有怪兽娘这么个东西，但一点也不了解。在电影院看到有上映此作，对其名字感兴趣，就看了。看了之后，我超喜欢这部作品！等熟肉什么时候出了，强烈建议大家一看。虽然我在11区电影院看此作时只能将人物对话连蒙带猜去理解，但是也基本能看明白此作内容。此作有趣极了，人物生动可爱，每个角色都是把奥特曼那些特摄片里怪兽娘化而成的。此作主要内容是以black为首的笨蛋三人组妄图征服世界，把此作的女主，即一个怪兽之魂还未觉醒的天真无邪的少女拉入自己一方，然后这四个人就谋划征服世界的计划，但是最终也没有得逞。此作的black的人设太赞啦！每一处的设定都是我喜欢的，欧派硕大，是能放在桌子上的那种，皮肤白皙，谷间的弧线和黑色衣服的映衬，显得魅力无穷。而且black的齐刘海黑长直的发型是我非常喜欢的，她那种头脑简单、本性善良但是表面上却喜欢作恶的性格也特别讨我喜欢，这点特别像乌贼娘。这真是一个令我难忘的角色，我太想拥有black啦！看这个电影时候会给赠品，角色是随机的，可惜我用两张票换来的两个赠品都不是black的，可惜了。此作基本能算是百合作，感觉最后black和女主之间很有百合气息，为了救女主也豁出去了。

哥斯拉（GODZILLA）噬星者
类型：剧场版
在电影院看到这个作品的名字时有点引起我的注意，而且看前面提到的动画的时候，在播放广告时，播了哥斯拉的预告，感觉挺壮观，像是大制作，再加上之前樋口真嗣和痞子导演的哥斯拉好像做得很厉害的样子，我为了打发时间就决定看此作。看了此作后，感觉比较失望，原来之前看到的那个不错的预告片的哥斯拉并不是这个哥斯拉。后来才得知原来此作编剧居然还是老虚，感觉老虚这次有点搞砸了。貌似此作有前作，但是前作没看过。看此作的时候，感觉前一半超级沉闷，一群男队员们一直在那里没完没了地说话，场景变化也少，看得我一头雾水，而哥斯拉就是不出现，坐在第一排的一个上年纪的人都睡着了，还打呼噜。而且此作是纯3D做的，画面渲染质量还不高，人物也没什么美感，要不然光看看画面也好。此作里有个很美型、身材高挑、沉着的反派，感觉有种《正解的卡多》里面那个外星人的感觉。此作里的女主倒还可以，看一群男人说话说半天，冒出来这么个女主，可算令乏味感还稍微减轻了点。后来哥斯拉好不容易终于出来了，被召唤来的三条火龙狂虐，啊啊啊~叫唤不停，感觉好可怜，虽然外表有点凶残，但看到它被这么蹂躏，真有点心疼。貌似此作里哥斯拉还算是“益怪”。最后经历了说不清道不明的过程，哥斯拉发大招把三条火龙干掉了，然后哥斯拉也安息了。此作结局真是莫名其妙，明明以男主为首的去外星球的队员们和当地的原住民都结婚生子了，居然最后男主还开着飞船撞向哥斯拉自尽，不愧是老虚写的剧本。

↧

GROMACS的安装方法（含全程视频演示）

January 2, 2019, 2:11 am

≫ Next: GROMACS的原生Windows版的编译和安装方法

≪ Previous: 2018年下半年观看的非TV版动画简评

GROMACS的安装方法

文/Sobereva@北京科音 2019-Jan-2

本文对最流行的分子动力学GROMACS程序在Linux下的安装方法进行详细说明。当新出的GROMACS版本的安装方法和本文所述出现较大差异时，本文也会做相应的更新。PS：之前笔者也写过老版本GROMACS安装方法，见《Gromacs 5.1.1与4.6.7编译方法》（http://sobereva.com/247）和《Gromacs 4.0.4、4.5.5版安装方法》（http://sobereva.com/29），但这俩文章对于目前版本来说已经没有意义了。

下面介绍的是GROMACS 2018.4版的安装，对GROMACS 2019经测试也完全适用，对于其它版本可能适用也可能不适用。本文是针对计算化学工作者最常用的CentOS 7.6操作系统写的，对于其它Linux系统的用户，安装方法可能与本文有异。本文的CentOS 7.6是按照《在VMware 15中安装CentOS 7.6的完整过程视频演示》（http://sobereva.com/454）演示的方式完全新装的。本文假定读者是root用户，程序将被安装到/sob目录下。如果你是普通用户，请随机应变，恰当设置路径。本文所示的安装过程中主机全程都能访问Internet。本文编译用的C++编译器是操作系统自带的gcc，虽然用Intel C++编译器也可以，但编译出的程序的速度没有显著差别。

下面安装的是纯CPU运算、单精度、能单机并行但不能跨节点并行的版本。如果需要GPU加速或跨节点或双精度运算，看文末的附注。用make的时候使用了-j选项以通过并行编译降低编译耗时，但个别情况下可能导致编译出错，届时请去掉-j再试。下文的安装过程有全程视频演示，初学者不熟悉Linux的话请严格效仿者安装：https://www.bilibili.com/video/av39749252/。

1 安装cmake 3.x

GROMACS 2018需要系统里有cmake 3.x才能编译。CentOS 7.6自带的cmake版本太老，因此需要先装cmake 3.x。

首先运行以下命令，添加EPEL源
yum install epel-release

然后在终端里输入yum install cmake3即可下载和安装cmake包，遇到提示的时候都输入y。之后输入cmake3命令看能否启动cmake3。

注：如果用yum的时候出现乱七八糟的提示安装不了，把操作系统重启一下往往就好了。

2 安装FFTW库

GROMACS 2018依赖于快速傅立叶变换库FFTW 3.3.8，可以在http://www.fftw.org/fftw-3.3.8.tar.gz下载。将其压缩包解压，进入此目录后运行
./configure --prefix=/sob/fftw338 --enable-sse2 --enable-avx --enable-float --enable-shared
以上语句代表FFTW将被安装到/sob/fftw338目录。如果你的CPU相对较新，支持AVX2指令集，可再加上--enable-avx2选项以获得更好性能。

然后运行make -j install开始编译，过一会儿编译完毕后，就出现了/sob/fftw338目录。然后可以把FFTW的解压目录和压缩包删掉了。

3 安装GROMACS

下载GROMACS 2018.4压缩包，地址为ftp://ftp.gromacs.org/pub/gromacs/gromacs-2018.4.tar.gz。然后将之拷到/sob目录下解压。进入解压后的目录，在终端里依次运行
mkdir build
cd build
export CMAKE_PREFIX_PATH=/sob/fftw338
cmake3 .. -DCMAKE_INSTALL_PREFIX=/sob/gmx2018.4
make install -j
Intel四核机子下，不到10分钟就能编译完毕。

此时程序就被编译和安装到了/sob/gmx2018.4目录下。修改用户目录下的.bashrc文件（比如运行gedit ~/.bashrc），在末尾加入source /sob/gmx2018.4/bin/GMXRC，然后保存。

之后关闭终端窗口，再次打开终端，输入gmx -version，看看是否输出了GROMACS的相关信息，是的话就说明安装成功了。之后可以把GROMACS压缩包和解压出来的目录删掉。

注1：在安装GROMACS过程中自动安装FFTW库

实际上，FFTW库可以不必手动安装，因为可以在安装GROMACS时自动下载并安装FFTW库。但由于国内链接FFTW官网服务器往往比较慢，自动下载FFTW库可能中途卡住或者过程巨慢，因此还是建议手动方式安装FFTW库。如果你确实打算自动安装FFTW库的话，将上文第2节直接忽略掉，也不必设export CMAKE_PREFIX_PATH=/sob/fftw338，把第3节的cmake3那一步额外加上-DGMX_BUILD_OWN_FFTW=ON选项即可，这样编译GROMACS时就会自动在FFTW官网上下载FFTW包并自动编译之。

注2：编译支持CUDA GPU加速的版本

GROMACS目前支持对nVidia的GPU通过CUDA方式的加速，也支持以OpenCL方式对其它厂商的GPU实现GPU加速。对于用CUDA方式加速，先去https://developer.nvidia.com/cuda-downloads下载CUDA toolkit并安装到默认路径，之后编译GROMACS方法同前，区别仅是cmake3这一步额外加上-DGMX_GPU=ON -DCUDA_TOOLKIT_ROOT_DIR=/usr/local/cuda选项（以实际CUDA tookit安装路径为准）
之后运行gmx mdrun运算时，会自动使用机子里的GPU进行加速。如果又不想使用GPU加速了，那还得按照上文方式编译一个只支持CPU运算的版本并放到不同的路径，并且把.bashrc改成source那个版本的GMXRC。

注3：编译双精度版本

一般计算只需要按照前述编译单精度版本就够了，但如果模拟刚开始就崩溃，有时候用双精度版本可解决，但计算比单精度版慢将近一倍、trr/edr等文件体积大一倍。另外，做正则振动分析时在能量极小化和对角化Hessian矩阵的时候一般也需要用双精度版以确保数值精度。注意，编译双精度版本时不支持GPU加速。

要编译双精度版本的话，先按照前文方式编译一遍单精度版本，毕竟这之后在研究中肯定也得用。然后再重复一遍编译过程，但是在编译FFTW时去掉--enable-float，并且在使用cmake3命令时额外加上-DGMX_DOUBLE=ON选项。双精度版本的GROMACS可执行文件是gmx_d，而单精度是gmx，因此单精度和双精度的可执行文件可以同时存在于同一目录，互不冲突。

注4：编译GROMACS的MPI版本

GROMACS跨节点并行计算需要MPI库，支持OpenMPI>=1.6、MPICH>=1.4.1。在编译这种GROMACS之前首先要安装MPI库，这里用OpenMPI。去http://www.open-mpi.org下载OpenMPI最新版本，解压并进入此目录后运行以下命令，就会编译并安装OpenMPI到/sob/openmpi目录：
./configure --prefix=/sob/openmpi
make all install -j
之后在用户目录下的.bashrc末尾加入以下两行
export PATH=$PATH:/sob/openmpi/bin
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/sob/openmpi/lib
然后重新进入终端使以上语句生效。之后编译GROMACS的方法同前，但在cmake3那一步额外加上-DGMX_MPI=ON选项。编译出来的可执行文件是gmx_mpi，比单机版本的可执行文件多了_mpi后缀。运行时候使用比如这样的命令：mpirun -np 16 gmx_mpi mdrun。
注：对于root用户，OpenMPI要求每次执行mpirun命令都得带着-allow-run-as-root选项才行，这很烦人，但可以通过在编译OpenMPI之前修改OpenMPI的源代码来避免，见《root用户在用openmpi并行计算时避免加--allow-run-as-root的方法》（http://sobereva.com/409）。

↧

GROMACS的原生Windows版的编译和安装方法

January 4, 2019, 5:05 am

≫ Next: 2018年下半年优秀动画音乐推荐

≪ Previous: GROMACS的安装方法（含全程视频演示）

GROMACS的原生Windows版的编译和安装方法

文/Sobereva@北京科音 2019-Jun-4

注：如果大家对编译过程不感兴趣，只想直接用原生Windows版的GROMACS，可以在http://sobereva.com/soft/gmx2018.4_win64.rar下载笔者编译好的原生Windows版GROMACS 2018.4，经测试Win7和Win10 64bit都可以用，安装方法见本文第3节。

1 前言：关于在Windows下使用GROMACS

GROMACS一般都是在Linux下运行，其Linux下的安装方法我在《GROMACS的安装方法》（http://sobereva.com/457）中已经详细交代了。在Windows下使用GROMACS有多种方式：
(1)使用VMware装Linux虚拟机，并照常以Linux方式编译。这十分简单，过程见《在VMware 15中安装CentOS 7.6的完整过程视频演示》（http://sobereva.com/454）。Linux下的所有程序都可以在以这种方式使用，非常普适，而且直接有图形环境。
(2)在Cygwin下编译。Cygwin提供了类似Linux系统的命令行环境，也提供了程序包管理器和源，相对于使用VMware更轻量级，而且编译出的程序只要提供一些Cygwin的dll文件就可以直接挪到其它Windows机子下用。对于大多数程序Cygwin下编译方式和Linux下一样（gcc、make、cmake等都有），但也有很多情况需要额外折腾，有时编译过程特别迟钝，而且有时候有一些特殊情况，比如笔者在Cygwin下编译GROMACS时必须要求不利用AVX指令集，否则编译会失败。
(3)Win10的Linux子系统。笔者个人不怎么喜欢这东西，这里不多提，和Cygwin在形式上有很大相似之处，鉴于是Windows自带的，以后必然会吞掉Cygwin很大的生存空间。
以上三种方法在原理上都会使得计算性能打一些折扣，但一般也就不到10%。
(4)编译原生的Windows版GROMACS。原理上来说，这是最完美的做法，编译出的程序可以拿到任何其它Windows机子上直接用，不需要装额外运行环境，而且在原理上也没有上述三种方法那样会对CPU性能打折扣。

本文就介绍一下怎么编译原生的Windows版GROMACS，过程相当简单。鉴于在Windows下使用GROMACS主要也就是偶尔图个方便才用，或者给初学者讲GROMACS时候用，极少会有Windows机子专门跑高耗时计算的情况，因此本文只介绍安装最普通形式的GROMACS的方法，即单精度、只能单节点并行、纯CPU版。

2 原生Windows版的编译过程

经测试，本文的过程对于GROMACS 2018.4和2019都适用。这里以2018.4为例。

首先安装Visual Studio，这里用的是Visual Studio 2017。VS2017最低级的是community（社区）版，是完全免费的。大家在https://visualstudio.microsoft.com/zh-hans/downloads/就可以下载到最新版。下载到的是一个非常小的安装器，启动它就可以在线安装（VS2017是没有镜像文件的。虽然也有办法把VS2017的组件全部下载后再离线安装，但是会占几十GB硬盘，因此不要考虑离线方式安装）。虽然看起来在线安装好像很耗时，但其实以现在的网速来说总耗时也不算很高。安装VS2017的时候应选择“使用C++的桌面开发”，确认“安装详细信息”中“用于CMake的Visual C++工具”是已选中的状态。

将gromacs-2018.4.tar.gz源代码包解压到比如C:\gromacs-2018.4。

在开始菜单里选Visual Studio 2017 - Visual Studio Tools - VS2017的开发人员命令行提示符，由此进入编译环境都配置好的命令行窗口。然后依次输入
cd C:\gromacs-2018.4
mkdir build
cd build
cmake .. -DCMAKE_INSTALL_PREFIX=C:\gmx2018.4 -DGMX_FFT_LIBRARY=fftpack -G "Visual Studio 15 2017 Win64"
cmake --build . --target INSTALL --config Release -j 4

过一阵子就编译好了，会出现C:\gmx2018.4目录，里面就是编译好的可执行文件以及相关文件了，内容和Linux版一样。

有几点值得进一步解释，对细节感兴趣者可以看看：

GROMACS需要利用FFT库，有三种选择
(1)FFTW库，这是最佳选择，Linux下编译都用FFTW
(2)MKL库，效率和FFTW差不多，需要额外安装
(3)fftpack库，这是GROMACS自带的，但效率相对低一些
上面为了省事，直接用了自带的fftpack库，实测比FFTW慢大概1/4左右。当然大家愿意折腾的话也可以自己在Windows下编译FFTW库或者安装MKL库并且连接之。虽然在Linux下编译GROMACS可以自动下载FFTW库并安装，但是在Windows下没法实现这点。

上面用的-j 4代表使用4核并行，机子里有几个物理核心建议就设几。

cmake的-G选项代表设置Generator，相当于指定编译环境，可以运行cmake -G查看有哪些Generator可选。"Visual Studio 15 2017 Win64"代表产生出对应于VS2017的64bit平台的解决方案，之后进而编译出的程序就是适合Windows 64bit的版本了。

如果读者打开build目录下的Gromacs.sln解决方案文件，会看到里面有很多不同的工程，其中名为ALL_BUILD的工程对应于编译出最终的可执行文件，而INSTALL的工程对应于不仅编译可执行文件，还将程序安装到CMAKE_INSTALL_PREFIX设的目录，因此上文的语句里用了--target INSTALL。

上面的--config后面跟的是编译时用的配置。名为Release的配置是适合用于发布的，会对代码充分进行优化。

3 原生Windows版的使用方法

注：如果你的计算机水平十分糟糕，难以正确按照以下文字操作，可参考演示视频：https://www.bilibili.com/video/av39914815/。

进入“控制面板”-“系统”，选择“高级系统设置”，在“高级”标签页里选择“环境变量”，在“xxx的用户变量”下面选择Path变量，点击“编辑”，在“变量值”文本框最后加上一个分号，然后再写上GROMACS目录的bin子目录的路径，比如;C:\gmx2018.4\bin。之后进入Windows的命令行窗口，输入gmx命令的时候就应该出现相关提示信息了，然后就可以像Linux版一样照常使用了。

↧

2018年下半年优秀动画音乐推荐

January 6, 2019, 5:17 pm

≫ Next: 2018年下半年优秀动画音乐推荐

≪ Previous: GROMACS的原生Windows版的编译和安装方法

2018年下半年优秀动画音乐推荐

文/Sobereva 2019-Jan-7

这是第9次写“优秀动画音乐推荐”系列文章，此系列从2014年起不断发布，致力于尽自己微薄之力，令最杰出、最美妙的音乐能有出头之地，而不被数目是它们20倍以上的海量的平庸、凑数的音乐埋没。之前的动画音乐推荐见
《2018年上半年优秀动画音乐推荐》（http://sobereva.com/428）
《2017年下半年优秀动画音乐推荐》（http://sobereva.com/405）
《2017年上半年优秀动画音乐推荐》（http://sobereva.com/385）
《2016年优秀动画音乐推荐》（http://sobereva.com/360）
《2015年下半年优秀动画音乐推荐》（http://sobereva.com/318）
《2015年上半年优秀动画音乐推荐》（http://sobereva.com/299）
《2014年下半年优秀动画音乐推荐》（http://sobereva.com/279）
《2014年上半年优秀动画音乐推荐》（http://sobereva.com/244）

这次推荐的音乐来自于笔者在2018年下半年期间听的动画相关的音乐，所有音乐都经过严格精挑细选。同人音乐都没有包含在内。有的音乐来虽然来自于老作品，但是恰好在这段期间内听到，也会被纳入推荐。推荐的不光来自于动画，还有一部分是CV或者日本歌手唱的，或者是游戏中的歌曲。

按照一直以来的习惯和对音乐的狂热执着，不管动画是否追了，所有新番的OST、OP/ED、歌曲集、角色集什么的一切衍生的音乐相关的产物笔者都是一个不落全仔细听完的，平均每天听3~4张，并将其中的精华留存到硬盘上，这个习惯从十几年前就开始了。

本次推荐的音乐下载地址：https://pan.baidu.com/s/1ex-H0fy2u5H97xga2WtPAw 提取码：1jws

音乐基本上都是我从无损或者320kbps mp3转成的176kbps ogg格式，此码率的ogg和320kbps mp3的音质没啥区别。ogg可以用foobar2000等播放器播放。笔者自己用的绿色版且主要插件都装齐的Foobar2000可以从此处下载：http://sobereva.com/soft/Foobar2000.rar。启动后需要对界面做一些设置来满足自己的习惯。Foobar2000是笔者认为的最优秀的音乐播放器，简洁小巧干净，该有的功能都有，又没有垃圾臃肿的功能。

动画音乐包含以下文件，共197首，807MB。Level B目录下的是虽然可圈可点，但整体还不算特别出色的音乐。

│ Basilisk ～樱花忍法帖～-愛する者よ、死に候え (実況録音版 ※2017 Live Version).ogg
│ Basilisk ～樱花忍法帖～-桜花忍法帖.ogg
│ Basilisk ～樱花忍法帖～-甲賀忍法帖 (実況録音版 ※2017 Live Version).ogg
│ Basilisk ～樱花忍法帖～-蛟龍の巫女 (実況録音版 ※2017 Live Version).ogg
│ DARLING in the FRANXX-トリカゴ.ogg
│ DEVILMAN crybaby-Devilman No Uta.ogg
│ DEVILMAN crybaby-Pathetique.ogg
│ Fate／EXTRA Last Encore ED-月と花束.ogg
│ あの空に還る未来で.ogg
│ 侧车搭档-Feel your breath(天野ありす＆伊藤くろす Ver.).ogg
│ 侧车搭档-Feel your breath(生駒女子高等学校).ogg
│ 剑王朝OP-宿業ノ剣.ogg
│ 带着智能手机闯荡异世界ED-スキノスキル.ogg
│ 灼热的乒乓球娘-Get Over.ogg
│ 灼热的乒乓球娘-Will.ogg
│ 灼热的乒乓球娘-真赤な誓い.ogg
│ 爱在雨过天晴后ED-Ref_rain.ogg
│ 覇穹封神演義ED-間遠い未来.ogg
│ 魔法使的新娘-Symphonic Poem “The Ancient Magus's Bride”.ogg
│ 魔法使的新娘-The Ancient Magus Bride's Main Theme.ogg
│ 魔法使的新娘-弓のアンソロジー.ogg
│
├─BanG Dream!
│      SURVIVOR　ねばーぎぶあっぷ!.ogg
│      もういちど　ルミナス.ogg
│      ピコっと！パピっと!! ガルパ☆ピコ!!!.ogg
│      二重の虹(ダブルレインボウ).ogg
│      最高(さあ行こう)！.ogg
│
├─level B
│ │ gdmen-妄想帝国蓄音機.ogg
│ │ Happy Sugar Life ED-SWEET HURT.ogg
│ │ Happy Sugar Life-ワンルームシュガーライフ.ogg
│ │ 刀剑乱舞-花丸-一対の火花、秘め事に触れ.ogg
│ │ 利兹与青鸟-lesson roomx.ogg
│ │ 利兹与青鸟-reflexion,allegretto,you.ogg
│ │ 利兹与青鸟-wind,glass,girls.ogg
│ │ 利兹与青鸟-物語の始まり.ogg
│ │ 动画同好会-アニメガタリズ?メインテーマ.ogg
│ │ 博多豚骨拉面团-DIRTY ROSES.ogg
│ │ 博多豚骨拉面团ED-DIRTY BULLET.ogg
│ │ 博多豚骨拉面团OP-ストレイ.ogg
│ │ 带着智能手机闯荡异世界OP-スライドライド.ogg
│ │ 废柴王子OP-D】D】D.ogg
│ │ 牙斗兽娘ED-ケダモノダモノ.ogg
│ │ 牙斗兽娘OP-killing bites.ogg
│ │ 犬屋敷ED-愛を教えてくれた君へ.ogg
│ │ 皇帝圣印战记OP-starry.ogg
│ │ 粗点心战争2-夏が終わる.ogg
│ │ 粗点心战争2-失意の果てに.ogg
│ │ 粗点心战争2-花火とほたる.ogg
│ │ 赛马娘-ゲートは今ひらく.ogg
│ │ 赛马娘-夢のゲートはいま開く.ogg
│ │ 赛马娘-心臓破りの坂.ogg
│ │ 齐木楠雄的灾难OP-ジャッジメント?ナイツ?オブ?サンダー～伝説の勇者.ogg
│ │
│ ├─刀使巫女
│ │      時にはトラブルも_.ogg
│ │      流れる涙は決意と共に.ogg
│ │      流れる涙は誰が為に.ogg
│ │
│ └─龙王的工作
│          あい登場.ogg
│          ゴッドコルドレン歩夢.ogg
│          一門の絆.ogg
│          八一、大逆転.ogg
│          天晴.ogg
│          師匠との日々.ogg
│          師匠の懐.ogg
│          幸先よく.ogg
│          独りじゃない.ogg
│          第一感.ogg
│          驚異の粘り.ogg
│
├─Love Live!Sunshine
│      Guilty!？ Farewell party.ogg
│      Thank you, FRIENDS!!.ogg
│      キセキヒカル.ogg
│      卒業ですね.ogg
│
├─Wake Up, Girls!
│      Wake Up, Girls! 新章 ED-雫の冠.ogg
│      Wake Up, Girls! 新章-同じ夢を見てる.ogg
│      Wake Up, Girls! 新章OP-7 Senses.ogg
│
├─偶像大师灰姑娘女孩
│      always.ogg
│      HARURUNRUN.ogg
│      if.ogg
│      Spring Screaming.ogg
│      Voyage.ogg
│      いとしーさー_.ogg
│      こいかぜ -紺碧-.ogg
│      未完成の歴史.ogg
│      踊りまくろ☆ダンシング?ナイト.ogg
│      銀河図書館.ogg
│
├─向山进发
│      intermission 楓のモノローグ.ogg
│      intermission 楓のモノローグ_2.ogg
│      ここな迷路～幻の小路～ .ogg
│      ここな迷路～幻の小路～.ogg
│      ひなたノスタルジア.ogg
│      メインテーマ.めぐりゆく季節に.ogg
│      メインテーマ.山に登るということ.ogg
│      メインテーマ?めぐりゆく季節に .ogg
│      向山进发ED-色違いの翼.ogg
│      大好きお母さん.ogg
│      思い出をたどって.ogg
│      泣きそうだよ.ogg
│      迷子の記憶 .ogg
│      追い風ホイッスル.ogg
│      駆け出す思い.ogg
│
├─告白实行委员会
│      Re_初恋の絵本.ogg
│      つまんないよ.ogg
│      センパイ。.ogg
│      不器用だから.ogg
│      好きと好きの方程式.ogg
│      明日は君と。.ogg
│      東京ウインターセッション.ogg
│      聞こえますか.ogg
│
├─在离别之朝竖起约定之花
│      イオルフ、別れの一族.ogg
│      ウィアートル.ogg
│      別れとの出会い.ogg
│      愛情の交錯.ogg
│      感謝と覚悟.ogg
│      母と子.ogg
│      母になる日々.ogg
│      生命と生命.ogg
│      約束の花.ogg
│
├─女皇之刃
│      Amara.ogg
│      buddy-body.ogg
│      Get the Door.ogg
│      maid in.ogg
│      my JUSTICE.ogg
│      命のうたが聞こえる.ogg
│      墜ちない空.ogg
│      大好きな場所.ogg
│      思い出と約束.ogg
│
├─少女歌剧
│ │ Circle of the Revue.ogg
│ │ Star Divine.ogg
│ │ The Star Knows.ogg
│ │ 世界を灰にするまで.ogg
│ │ 少女歌剧ED-Fly Me to the Star.ogg
│ │ 少女歌剧OP-星のダイアローグ.ogg
│ │ 花咲か唄.ogg
│ │ 誇りと驕り.ogg
│ │
│ └─「少女☆歌劇レヴュースタァライト ―The LIVE―」#1 revival
│          3?7?5?1?0.ogg
│          Glittering Stars.ogg
│          Resist.ogg
│          RE_.ogg
│          ジャンヌダルク.ogg
│          ポジションゼロへ！.ogg
│          私たちの居る理由.ogg
│
├─悠哉日常大王
│      いつかまた.ogg
│      散歩道.ogg
│
├─擅长捉弄的高木同学Cover Song Collection
│      AM11_00.ogg
│      出逢った頃のように.ogg
│      小さな恋のうた.ogg
│      愛唄.ogg
│      自転車.ogg
│      風吹けば恋.ogg
│
├─比宇宙更远的地方
│      Bon Voyage! ~Main Theme~..ogg
│      任務遂行.ogg
│      南極の太陽.ogg
│      大人からのYell.ogg
│      最後まで諦めない.ogg
│      状況説.ogg
│      私たちは必ず南極に行く.ogg
│
├─紫罗兰永恒花园
│      A Doll's Beginning.ogg
│      A Place to Call Home.ogg
│      A Simple Mission.ogg
│      Across the Violet Sky.ogg
│      An Admirable Doll.ogg
│      Another Sunny Day.ogg
│      Back in Business.ogg
│      Believe in….ogg
│      Each Memory a Message.ogg
│      Honest Times.ogg
│      In Remembrance.ogg
│      Ink to Paper.ogg
│      Letter.ogg
│      Lost child.ogg
│      Never Coming Back.ogg
│      One Last Message.ogg
│      Rust.ogg
│      Strangeling.ogg
│      The Birth of a Legend.ogg
│      The Long Night.ogg
│      The Love That Binds Us.ogg
│      The Voice in My Heart.ogg
│      Theme of Violet Evergarden.ogg
│      Those Words You Spoke to Me.ogg
│      To The Ends of Our World.ogg
│      Unspoken Words.ogg
│      Violet Snow for Orchestra.ogg
│      Violet's Letter.ogg
│      女神の祈り -Requiem-.ogg
│      紫罗兰永恒花园ED-みちしるべ.ogg
│      紫罗兰永恒花园OP-Sincerely.ogg
│
├─蓝海少女第二季
│      CHAKOMON.ogg
│      出会いと別れ.ogg
│      夕涼み.ogg
│      幸せの達人.ogg
│      幻想のカノン.ogg
│      海と空と太陽と～epilogue～.ogg
│      海と空と太陽と～sunshower～.ogg
│
└─音乐少女
        be with you.ogg
        terzetto rhapsody.ogg
        You are my only one.ogg
        スタートライン.ogg
        フライガール.ogg
        太陽(てぃーだ)の花.ogg

非动画音乐包含以下曲目，共21首，106MB。

Aimer-Raining.ogg
ASCA-グラヴィティ with fox capture plan.ogg
BREAKERZ-GREAT AMBITIOUS -Single Version-.ogg
BREAKERZ-ポジティブブルー～Acoustic Version～.ogg
CHiCO with HoneyWorks-ラズベリー＊モンスター.ogg
ReoNa-カナリア.ogg
Run Girls, Run!-サクラジェラート.ogg
あゆみくりかまき-泣き顔笑顔.ogg
つりビット-ハピハピフィッシングデート.ogg
つりビット-不思議な旅はつづくのさ.ogg
やなぎなぎ-想像の君.ogg
イケてるハーツ-Distance Love.ogg
イケてるハーツ-希望の地図.ogg
ナナヲアカリ-なんとかなるくない_.ogg
ナナヲアカリ-愛の歌なんて.ogg
中岛美嘉-GLAMOROUS SKY (Re_Present 2018).ogg
卓球と旅人-今夜だけ.ogg
喜多村英梨-fairy∞world.ogg
早见纱织-琥珀糖.ogg
竹达彩奈-セピア色.ogg
綾野ましろ-LAST FUTURE.ogg

↧

2018年下半年优秀动画音乐推荐

January 6, 2019, 5:17 pm

≫ Next: 简谈Gaussian里找过渡态的关键词opt=TS和QST2、3

≪ Previous: 2018年下半年优秀动画音乐推荐

2018年下半年优秀动画音乐推荐

文/Sobereva 2019-Jan-7

本次推荐的音乐下载地址：https://pan.baidu.com/s/1ex-H0fy2u5H97xga2WtPAw 提取码：1jws

动画音乐包含以下文件，共197首，807MB。Level B目录下的是虽然可圈可点，但整体还不算特别出色的音乐。

非动画音乐包含以下曲目，共21首，106MB。

↧

简谈Gaussian里找过渡态的关键词opt=TS和QST2、3

February 3, 2019, 6:31 am

≫ Next: 使用Multiwfn计算CVB指数考察氢键强度

≪ Previous: 2018年下半年优秀动画音乐推荐

简谈Gaussian里找过渡态的关键词opt=TS和QST2、3

Sobereva@北京科音文/2019-Feb-3

Gaussian里找过渡态的关键词有三：opt=TS、opt=QST2、opt=QST3。经常在网上看到有很多初学者居然把QST2当做找过渡态默认用的关键词，明显是被一些坑爹言论毒害的后果。这里就抽一点时间非常简单地说说常用的opt=TS关键词，以及为什么我很不建议在一般情况下用QST2、QST3。本文并不举实际计算例子，我认为学习找过渡态得通过大量例子才能培养出感觉（这方面内容在北京科音初级和基础量子化学培训班里都会讲得很详细，并且会给出一大把各种类型反应例子，详见http://sobereva.com/355）。关于过渡态搜索的算法，感兴趣者看《过渡态、反应路径的计算方法及相关问题》（http://sobereva.com/44）。

1 关于opt=TS

一般情况下我都建议用opt=TS找过渡态，其算法和优化极小点结构非常类似，只不过它要求优化的是势能面的一阶鞍点。具体来说一般是用opt(TS,calcfc,noeigen)关键词，calcfc代表精确计算初始结构的Hessian矩阵，noeigen代表优化过程中不对每一步做Hessian矩阵本征值数目的检测（这个要求太严而且没太大必要）。用opt=TS只需要提供一个初猜的过渡态结构就够了，很方便。只要初猜结构和实际过渡态比较接近，而且计算级别和模型合理，一般都能收敛到实际过渡态。一般建议再同时写上freq关键词使得优化结束后自动做个振动分析。

怎么验证过渡态找没找对？如果优化出来的过渡态结构在期望的反应物和产物之间，同时有且只有一个虚频，一般能有6成把握认为过渡态找对了。如果通过gview查看，发现仅有的那个虚频的振动方向对应反应坐标方向，那8成可以认为过渡态找对了；如果走IRC还能连通自己期望的反应物和产物结构，那么说明100%找对了。走IRC的相关信息看《在Gaussian中计算IRC的方法和常见问题》（http://sobereva.com/400）。

opt=TS常见问题如下：
·如果优化出现震荡、难收敛，但是用gview观看结构变化感觉收敛趋势对，可确认优化过程是在往过渡态模样的结构走，最后一帧结构有过渡态的大致模样，按照《量子化学计算中帮助几何优化收敛的常用方法》（http://sobereva.com/164）适当处理即可。
·如果是找出来的过渡态不仅存在一个对应反应坐标方向的虚频，还存在额外的虚频，按照《Gaussian中几何优化收敛后Freq时出现NO或虚频的原因和解决方法》（http://sobereva.com/278）消除多余虚频即可。
·如果优化不收敛或者报错，且最后一帧结构完全不像实际过渡态，或者虽然任务正常结束了但是根本都没有虚频，或者虽然只有一个虚频但是并不是对应当前反应方向的，那就是说明自己提供的初猜结构不合理（也有可能是计算级别不合理，导致当前级别势能面上根本没有对应实际过渡态的一阶鞍点），那就再反复尝试其它自己觉得靠谱的初猜结构，或尝试其它自己觉得合理的计算级别。

找过渡态和优化极小点一样，不需要用到太昂贵的计算级别，见《浅谈为什么优化和振动分析不需要用大基组》（http://sobereva.com/387）。找过渡态和优化极小点用的计算级别应当一致，因为并没有用不同级别的合理理由。对于溶剂下的反应，特别是极性溶剂下，优化过渡态的时候最好就带着隐式溶剂模型，因为有的时候可能有定性影响。对于某些反应，溶剂可能直接影响反应机理，此时用隐式溶剂模型时还得同时用显式溶剂模型。

哪怕是有丰富经验的研究者，也没有那个敢打包票说看见一个反应就能保证一次就找到过渡态。找过渡态的难度远大于优化极小点，因为对初猜结构要求高。显然初学者不应当因为对于一个反应尝试了几个过渡态初猜都失败就简简单单放弃，或者投奔QST2。如果体系比较大，每次试初猜都比较耗时，可以先用更便宜但对于当前体系也能给出定性合理结果的计算级别，等收敛到了期望的过渡态，再把这个结构当做过渡态初猜，结合用原本打算用的更好的级别去进一步准确优化过渡态。其实对于大部分有机反应（也有很多例外），用PM6、PM7这样的极便宜的半经验方法就可以给出定性合理的过渡态结构，由于很便宜，因此建议同时加上calcall增加收敛成功的几率。另外也可以考虑尝试用现在很火的Grimme的GFN-xTB，普适性比半经验方法更好而且速度飞快，见《将Gaussian与Grimme的xtb程序联用搜索过渡态、产生IRC、做振动分析》（http://sobereva.com/421）。

2 关于QST2、3

网上有一堆乌七八糟的Gaussian学习资料，还有官方的exploring那本书的第3版，给初学净拿QST2举例子，对opt=TS居然反倒不怎么提，导致初学者以为Gaussian里找过渡态本来就应该用QST2，有经验的人都知道这真是赤果果地在坑初学者。相对于最常用的opt=TS，用QST2有很大弊端：
(1)使用QST2必须同时提供要研究的基元过程的反应物和产物的结构（不需要很精确也不需要非得事先优化，只要模样差不多对就可以）。这比起opt=TS只需要提供一个过渡态初猜结构显然在准备工作上更麻烦。而且有些情况你根本都不好估计其中一方是什么结构。比如双分子反应（或单分子裂解反应），你往往根本就不知道反应复合物（或产物复合物）长什么样子，得找出过渡态之后走完IRC才知道，如果你试图去猜的话，这比起你用opt=TS且直接给个合理的过渡态初猜的难度通常更大。
(2)用户必须确保提供的反应物和产物结构间原子顺序完全对应，否则任务一定失败，而保证这点往往很麻烦。虽然gview里提供了connection工具可以辅助你去把两帧结构里的原子顺序进行自动匹配，但是也往往匹配不成功，或者虽然表面上告诉你匹配成功了但其实还是有原子根本没有正确匹配，你还得手动根据两帧的结构图和原子序号通过反复交换原子使顺序一致，相当费事！
(3)QST2本身不是不需要过渡态初猜结构，只不过QST2计算过程中过渡态初猜结构是程序根据你提供的反应物和产物坐标根据插值产生出来的（优化过程中QST2算法还会根据反应物和产物结构对优化方向进行引导）。这样简单粗暴、机械化产生的过渡态结构，怎么可能比起有基本化学直觉的人摆出来的过渡态初猜结构更合理？QST2用多了你就会发现，QST2自动产生的初猜往往很差劲，虽然有时候很烂的初猜结构最终还是收敛到了实际过渡态，但是达到收敛所需的步数明显高于你用opt=TS并直接提供一个基本靠谱的过渡态初猜，因此浪费了很多计算时间。还有的时候，哪怕你提供的反应物和产物结构基本和实际相符，QST2也会给出一个一看就离谱的初猜结构，导致根本不可能收敛到实际过渡态去（即便QST2还会利用反应物和产物结构来引导优化也于事无补）。
(4)Gaussian的QST2代码本身也往往有问题，有时候明明输入文件完全正确，但是算起来却会莫名其妙报错。

老有一些初学者净以为QST2是万灵药，好像给了反应物和产物结构就一定能找出对应的过渡态，明显这是极度荒唐的，QST2可能哪有这么聪明？甚至于，实验上发现反应物A最终转化到产物B，而且一看就不是一个基元过程，居然有的初学者也拿A和B的结构直接输到Gaussian里跑QST2。这么做，整个复合反应中哪个过渡态的结构都优化不出来！PS：目前倒是也有一些自动找过渡态的算法，比如GSM、GRRM等等，思想、流程都远比QST2要复杂得多，可参考《寻找势能面上全部极小点、过渡态的算法GRRM简介》（http://sobereva.com/319）、WIREs Comput. Mol. Sci., e1354 (2017)、J. Chem. Theory Comput., 13, 5780 (2017)。

还有初学者用QST2的理由是“opt=TS算不出来”。我特别讨厌“算不出来”这种含糊不清的描述，因为等于什么都没说。要知道，只要恰当地使用opt=TS，什么反应的过渡态都能算出来！原理上，opt=TS找不出来的过渡态，用QST2也绝对不可能找到。如果你已经基于基本合理的过渡态初猜结构、在合理的设定下正确地做opt=TS任务，最终也没找出来过渡态，那么指望用QST2就能找出来你想要的过渡态，概率等于连续三次单抽都出UR。

QST2也不是一无是处，在恰当的时候使用也能帮助你更方便地找过渡态，但前提必须是你已经能够熟练使用opt=TS找过渡态，而且已经充分了解QST2的思想和优缺点。可以用QST2的情况有下：
(1)虽然你的头脑里知道要找的过渡态大概长什么样，自己在gview里慢慢摆也能摆出来其合适的初猜，但是涉及的几何变量太多，摆起来太花时间或者确实就是不好操作，与此同时反应物和产物的大致结构比较好确定、也容易确保原子顺序对应，那么可以先尝试用QST2，没准直接能优化到过渡态，从而节约了你反复尝试摆合理过渡态初猜的时间。
(2)对于一个基元反应，限于你的化学直觉，实在不知道过渡态应该长什么样，你可以用QST2碰运气，但是绝对不要抱太大期望。

值得一提的是，QST2计算的时候不需要像opt=TS那样需要由用户提供初始的Hessian，即哪怕calcfc都可以不写，因此对于Gaussian里一些没二阶解析导数的方法如CCSD也可以用（当然了，在CCSD级别下找过渡态一般是愚蠢的做法，贼贵而且没必要），也可以避免一些后HF方法在计算解析Hessian时的高昂代价。不过，QST2关键词里也写上calcfc（或者更贵也更好的recalc=x、calcall）有助于增加收敛到过渡态的几率。
PS：其实opt=TS也不是必须得明确提供初始的Hessian，比如用opt(TS,modRedundant,noeigen)或者opt(TS,gediis,noeigen)的话也可以不用calcfc，但当然收敛成功的几率要明显低于opt(TS,calcfc,noeigen)。

至于QST3，不仅像QST2一样需要提供反应物和产物结构，还得再提供过渡态初猜结构，麻烦得要死，而收敛到过渡态的成功几率并不比直接用opt=TS强多少，基本没有实际价值，因此无需考虑。

opt=TS、QST2、QST3找出来的过渡态结构在原理上是没有差别的。因此，不管用的哪种方法去找，只要最终的结构通过前面提到的方式验证可以确定找对了，那就绝对没有必要再用另外的方法再去计算一次。

↧

使用Multiwfn计算CVB指数考察氢键强度

February 4, 2019, 11:32 pm

≫ Next: 使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱

≪ Previous: 简谈Gaussian里找过渡态的关键词opt=TS和QST2、3

使用Multiwfn计算CVB指数考察氢键强度

文/Sobereva@北京科音

First release: 2019-Feb-5 Last update: 2019-Feb-6

摘要：本文介绍基于电子定域化函数(ELF)定义的用于衡量氢键强度的CVB指数，并且演示怎么在Multiwfn程序（http://sobereva.com/multiwfn）中计算。掌握这个方法，在讨论氢键问题的时候相当于多了一个很有用的工具。

1 CVB指数的思想以及计算方法

core-valence bifurcation (CVB)指数是最初在Theor. Chem. Acc., 104,13 (2000)中由Silvi等人提出的一种考察氢键强度的方法，它利用了电子定域化函数(ELF)的拓扑分析的思想。如果对ELF不熟悉的话，请参阅《ELF综述和重要文献小合集》（http://bbs.keinsci.com/thread-2100-1-1.html）。后来有不少文章都使用了这个指数讨论氢键，比如Struct. Chem., 16, 203 (2005)、J. Phys. Chem. A, 115, 10078 (2011)，在一篇从理论角度分析氢键的综述Chem. Rev., 111, 2597 (2011)中也对CVB指数进行了介绍。

一般的氢键可以写为D-H...A的形式，其中D是氢键给体原子（donor），A是氢键受体原子（acceptor）。用ELF盆分析的语言来描述的话，这块区域由以下的ELF盆构成：
V(D,H)：D和与之成键的H共同构成的价层(valence)盆
C(D)和C(A)：D原子和A原子的内核(core)盆
V(A)：A原子的价层盆
相邻的盆之间都有所谓的二分点(bifurcation point)，对应于拓扑分析语言里的(3,-1)型ELF临界点。如果你不懂什么叫二分点、不懂怎么计算的话，可以看看《在Multiwfn中单独考察pi电子结构特征》（http://sobereva.com/432）一文中对ELF-pi函数考察其二分点的例子，本文第四节的例子也通过ELF拓扑分析考察了二分点。

CVB指数在Theor. Chem. Acc.那篇文章中的定义为：CVB index = ELF(C-V) - ELF(DH-A)
其中ELF(C-V)代表内核盆与价层盆之间的二分点数值，ELF(DH-A)代表V(D,H)与V(A)之间的二分点数值，也即H与A原子间(3,-1)型ELF临界点的ELF数值。CVB指数越负，通常氢键越强，这点在原文以后后续一些文章里都通过实例进行了验证。比较强的氢键的CVB指数一般明显为负；极强、带有明显共价特征的氢键可以达到很负的数值；中等强度氢键的CVB指数一般在0附近；较弱的氢键的CVB指数一般明显为正。其实为什么会这样也不难理解，因为氢键越强，H和A之间的距离通常越近，H...A作用的共价性也会越显著，势必ELF(DH-A)会越大、导致CVB index越负。其实说白了，CVB指数的名字虽然重在core-valence二分点数值，但真正关键的其实是ELF(DH-A)的数值，不同氢键的ELF(DH-A)的差异远比ELF(C-V)大得多得多。

在CVB指数的原文里，对CVB指数的计算细节没有说清楚，这导致之后不同文章在计算CVB指数的时候用的具体做法不同，而且CVB指数原文里的数据还存在错误，尤为明显的错误是把符号搞反了，而且在后来的某些相关文章中和CVB有关的叙述还往往是错的，总之被搞得一团糟，那些文章里的CVB数值也很难或根本无法重现出来。

笔者在Multiwfn里专门加入了CVB指数的自动计算功能，是主功能200的子功能1，只要输入D、H、A原子的序号即可计算。在Multiwfn中计算CVB指数的做法是笔者提出来的，笔者认为这种方式计算不仅耗时很低（基本上秒算）、操作极简单、实现极容易，而且意义明确。

在Multiwfn的这个功能中，CVB指数定义为：CVB index = ELF(C-V,D) - ELF(DH-A)
其中，ELF(DH-A)不是通过拓扑分析搜索出来的精确的V(D,H)与V(A)之间的二分点的数值，而是在H-A连线上计算ELF曲线，从中取H和A之间ELF极小点的数值，因为这样计算容易得多。而且由于精确的二分点位置几乎就在H-A的连线上，因此Multiwfn中这种近似方式得到的ELF(DH-A)与按照CVB指数原始定义计算的ELF(DH-A)几乎没有差异。
上式中ELF(C-V,D)的物理意义是D原子上的core-valence二分点数值。Multiwfn中虽然也可以通过其强大的拓扑分析功能（主功能2）得到准确的这种二分点位置和数值，但这种二分点在实际中往往不好考察，同一个原子可能有多个这样的二分点，在选取上有任意性。而且如果是第二周期之后的原子，二分点会更多，考察时更麻烦。而且笔者也认为，用精确的二分点也并没有太强的物理意义，因为它们往往都不在D-H连线方向上，因此和氢键特征也联系不紧密。考虑到这些，在Multiwfn自动计算CVB指数的功能中，ELF(C-V,D)是直接取D-H连线上相应的ELF极小点数值。

Multiwfn自动计算CVB指数的功能中会计算三个量，思想很简单，如下所示：

实际上你也完全可以通过主功能3来绘制ELF曲线（例子看Multiwfn手册4.3节），并让程序给出极小点位置和数值，由此手动得到CVB指数，只不过使用Multiwfn自动计算CVB指数的功能在操作上方便得多。上图中顺带搜索到的ELF(C-V,A)并没什么实际用处，但是可能有的用户对此感兴趣，所以程序也会顺带输出。

由于Theor. Chem. Acc.那篇文章里的数据有一定问题，而且对测试体系计算氢键结合能用的级别在现在来看非常烂（B3LYP/6-31G**），因此文中的数据不足为信。笔者用这篇文章里的一部分氢键二聚体，在可靠的B3LYP-D3(BJ)/def2-TZVP下优化并得到波函数文件，使用Multiwfn自动计算CVB指数的功能做了计算，并且用计算氢键结合能精度很高的MP2/jul-cc-pVQZ结合counterpoise校正计算了氢键结合能，结果如下

可见，CVB指数和氢键结合能之间的线性关系虽然不算完美，但线性关系还是很显著的。如果把OC...HF这个例外不计的话，那么线性关系就很理想了。

其实，CVB指数的两个组成部分自身也与氢键强度存在明显相关性（起码对这批体系而言），如下所示

由于“CVB指数 vs 结合能”的图和“ELF(DH-A) vs 结合能”很相似，所以CVB指数的重点是ELF(DH-A)，哪怕忽略ELF(C-V,D)其实也无大碍。ELF(C-V,D)与结合能的线性关系很好，但并不好从物理意义上解释原因，同时也可以看到对不同氢键其数值差异很小。总之，当你用CVB指数讨论氢键的时候，也可以顺带检验一下其两个组成部分和氢键强度的相关性。

还值得一提的是，对这些氢键二聚体，笔者发现AIM理论里的键临界点(BCP)的电子密度ρ(BCP)和结合能的关系颇好，如下所示（笔者也考察了BCP处势能密度，发现与结合能的线性关系远没有这么好）。ρ(BCP)用Multiwfn可以非常容易地计算，见《使用Multiwfn做拓扑分析以及计算孤对电子角度》（http://sobereva.com/108）。AIM的相关知识看《AIM学习资料和重要文献合集》（http://bbs.keinsci.com/thread-362-1-1.html）。

2 CVB指数在Multiwfn中的计算一例：HF...HF

只有在2019-Feb-5及之后更新的Multiwfn中才有CVB指数自动计算功能。不了解Multiwfn的话看《Multiwfn入门tips》（http://sobereva.com/167），不知道怎么产生Multiwfn需要的输入文件的话看《详谈Multiwfn支持的输入文件类型、产生方法以及相互转换》（http://sobereva.com/379）。常见的.fch、.molden、.wfn等格式都可以作为CVB指数计算功能的输入文件。

下面以HF...HF作为例子演示在Multiwfn中计算CVB指数，由Gaussian 16 A.03在B3LYP-D3(BJ)/def2-TZVP下优化并产生的wfn文件是examples目录下的HF_HF.wfn，体系结构如下

启动Multiwfn，输入
examples\HF_HF.wfn
200 // 其它功能(part2)
1 // 计算CVB指数和相关的量
2,1,3 //氢键给体原子、氢原子和氢键受体原子的序号

输出信息如下
Core-valence bifurcation value at donor, ELF(C-V,D): 0.0936
Distance between corresponding minimum and the hydrogen: 0.743 Angstrom

Core-valence bifurcation value at acceptor, ELF(C-V,A): 0.1408
Distance between corresponding minimum and the hydrogen: 1.628 Angstrom

Bifurcation value at H-bond, ELF(DH-A): 0.0648
Distance between corresponding minimum and the hydrogen: 0.614 Angstrom

The CVB index, namely ELF(C-V,D) - ELF(DH-A): 0.028768

各项是什么含义，只要仔细看了上一节就肯定明白。输出中还顺便把相应的ELF曲线极小点与氢原子之间的距离显示了出来。

3 某些极强氢键的特殊考虑

对于某些极强的氢键，由于H和A之间的作用也非常强，存在显著共价特征，此时V(D,H)二分为V(D)和V(H)，例如下图所示的体系（由于O-H-F基本在一条直线上，所以就不把O-H和H-F的ELF曲线图单独绘制了，而是为了省事直接绘制O-F连线上的图）。

此体系中，由于F形式上是以F-阴离子形态存在，与带正电的氢的作用极强，这使H和F之间已经存在不可忽视的共价性（而一般氢键的主要本质是静电作用），因此在对应的二分点C位置，ELF数值远大于一般强度氢键的情况。H与F强烈吸引，导致水分子中的O3-H2键遭到很大破坏，拉长了O3-H2的距离，也同时导致V(H2)独立的ELF盆的出现，因此曲线上出现了极小点A。

像上面这种明显不具备典型D-H...A氢键特征的体系，前述的Multiwfn的CVB指数自动计算方法是明显不适用的，强行用的话结果是没意义的，必须通过主功能3作图并手动计算。这个体系可以认为存在两种氢键O-H...F和O...H-F，二者的结合能存在明显差异，其CVB指数在计算的时候也应当分别考虑：
考察O-H...F时，CVB index = ELF(B) - ELF(C)
考察O...H-F时，CVB index = ELF(D) - ELF(A)
由于ELF(B)和ELF(D)差不太多，而ELF(A)显著大于ELF(C)，因此O...H-F的CVB指数明显更负，体现O...H-F的结合强度比O-H...F肯定大得多。

在Multiwfn手册的3.200.1节当中还有关于CVB指数更多的信息，有兴趣的读者建议看看。

4 氢键受体不是单一原子情况时CVB指数的计算

有很多氢键的受体并不是特定的某个原子，比如pi-氢键，是以富集的pi电子云作为氢键受体。这种情况下，也没法用前述的Multiwfn中自动计算CVB指数的功能来计算，而需要根据实际情况手动进行计算。这里以HF...乙烯二聚体作为例子。B3LYP-D3(BJ)/def2-TZVP下优化并产生的波函数文件是examples目录下的C2H4_HF.wfn。其结构如下

先计算ELF(C-V,D)。按照之前用到的做法，在F7-H8连线方向上绘制ELF，查看对应的极小点即可。启动Multiwfn并输入
examples\C2H4_HF.wfn
3 //绘制曲线图
9 //绘制ELF
0 //设定延展距离
0 //延展距离设为0（使得图的两端正好是两个原子核位置）
1 //输入两个原子序号定义直线
7,8
把弹出来的图关闭，后处理菜单选择6，在屏幕上看到
Minimum X (Bohr): 0.356648 Value: 0.94377038E-01
这个极小点的数值0.0944即是ELF(C-V,D)。

对于当前体系的ELF(DH-A)，我们应当通过做ELF拓扑分析找到对应H8与乙烯pi区域之间的ELF二分点位置来得到其数值。接着在Multiwfn里输入
0 //返回主菜单
2 //拓扑分析
-11 //选择要做拓扑分析的函数
9 //ELF
6 //在特定圆球内随机撒初猜点的方式找临界点
4 //将圆球中心定义为三个原子的中点
1,4,8 //将C1,C4,H8的中心作为圆球的中点，这时圆球的区域内理应会包含当前要找的氢键处的ELF二分点
0 //开始在圆球内随机撒初猜点来找临界点（撒的点数可以事先通过选项11设定，圆球半径也可以自设）
-9 //返回拓扑分析主界面
0 //观看临界点分布
看到的图如下所示，为了清楚，这里只显示出(3,-1)和(3,-3)型ELF临界点，分别是桔球和紫球。

我们看到在H8与pi电子区域之间找到了ELF二分点，即5号临界点。点右上角的RETURN退出图形窗口，选择选项7考察临界点属性，再输入5，在屏幕上看到
Electron localization function (ELF): 0.1240943921E+00
即此体系氢键的ELF(DH-A)=0.1241。因此，此氢键的CVB指数为0.0944-0.1241=-0.0297。

由于这个体系对称性较高，其实不做拓扑分析也可以得到ELF(DH-A)，也就是用主功能3绘制H8与C1-C4的中点连线上的ELF曲线，然后从中取对应的极小点，数值和上面做拓扑分析得到的完全一致。但如果体系对称性不那么高，显然就没法这么通过ELF曲线图比较准确地得到实际二分点位置的ELF值了。

↧

使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱

February 9, 2019, 6:22 pm

≫ Next: 量子化学程序Dalton的编译方法和运行方式简介

≪ Previous: 使用Multiwfn计算CVB指数考察氢键强度

使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱

文/Sobereva@北京科音 2019-Feb-10

1 前言

看本文前，强烈建议先看《使用Gaussian+PySOC在TDDFT下计算旋轨耦合矩阵元》（http://sobereva.com/411）了解一些旋轨耦合矩阵元计算的基本知识，以及看《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》（http://sobereva.com/314）了解TDDFT计算的相关知识。TDDFT和旋轨耦合(Spin-orbit coupling, SOC)方面的理论性的内容在本文就不多提了，笔者假设读者已经看了上面两篇具备了相关常识。如果你不会装ORCA，看《量子化学程序ORCA的安装方法》（http://sobereva.com/451）。

从ORCA 4.1开始，ORCA支持了TDDFT下闭壳层体系的旋轨耦合的计算，可以做的相关的事包括：
·计算旋轨耦合矩阵元
·计算旋轨耦合对基态和激发态能量的影响
·计算考虑旋轨耦合时的振子强度和转子强度，结合Multiwfn可以绘制考虑旋轨耦合后的光谱
本文就对ORCA的TDDFT的旋轨耦合计算进行基本介绍，其中最主要是讲旋轨耦合矩阵元的计算和绘制旋轨耦合校正的UV-Vis光谱，最后也简单谈一下用ORCA的这种SOC-TDDFT计算有无可能给出靠谱的磷光发射速率的问题。

使用ORCA在TDDFT下计算旋轨耦合矩阵元相对于使用之前笔者介绍的Gaussian+PySOC的组合有下列好处：
(1)ORCA开RI的时候做TDDFT计算本身远比Gaussian快得多，除很小体系外至少快一倍，而气相的结果可以与Gaussian很好相符
(2)ORCA对学术用户完全免费
(3)PySOC只能用较low的有效核电荷(Zeff)方式考虑旋轨耦合。而ORCA不仅支持Zeff，还支持更精确的旋轨耦合平均场(SOMF)方式考虑
(4)PySOC大部分是Fortran写的，有一小部分莫名其妙地偏要用Python编写，导致在Windows下运行不方便，而很多操作系统下由于Python版本原因导致PySOC运行不成功。而ORCA在所有操作系统下都能顺利运行
(5)用ORCA计算比用Gaussian+PySOC的组合方便不少，而且还省得让Gaussian往硬盘里保存很占地方的rwf文件
总的来说，ORCA算是目前在TDDFT下计算旋轨耦合矩阵元最理想的程序。

下面结合实例介绍ORCA的SOC-TDDFT计算。涉及的输入输出文件都可以在此处下载：http://sobereva.com/attach/461/file.rar。本文用的是ORCA 4.1.1。

2 旋轨耦合矩阵元计算实例1：甲醛

首先用一个非常简单的体系甲醛来说明怎么在ORCA里做考虑了旋轨耦合的TDDFT计算、怎么去理解输出。

下面这个输入文件对甲醛在B3LYP/def-TZVP下做TDDFT计算。几何结构已经在PBE0/def-TZVP级别下优化过。
! B3LYP/G TZVP miniprint tightSCF grid4 pal4
%tddft
nroots 5
dosoc true
tda false
printlevel 3
end
* xyz 0 1
C                  0.00000000    0.00000000   -0.52513500
H                  0.00000000    0.93987900   -1.11261300
H                  0.00000000   -0.93987900   -1.11261300
O                  0.00000000    0.00000000    0.67200400
*

之所以此例在B3LYP后面写了个/G，是因为ORCA里默认的B3LYP与Gaussian的B3LYP不同，加/G代表我们这里想使用与Gaussian相同的B3LYP定义。TZVP代表用def-TZVP基组，和Gaussian里写TZVP时用的基组相同。miniprint代表不输出一堆乱七八糟没太大用的信息（尤其是布居分析，又占地方又不好读，而用笔者开发的Multiwfn随时都可以基于ORCA产生的.molden文件做更丰富的布居分析，而且分析起来方便得多）。tightSCF代表用比默认更严的SCF收敛限，对于涉及到后HF、TDDFT等多组态方法的时候都建议加上。grid4代表用比默认更好的DFT积分格点，这有助于降低数值误差。pal4代表用4核并行。%tddft...end段落代表做TDDFT计算，dosoc true代表TDDFT计算过程考虑旋轨耦合效应。ORCA默认做TDDFT时候是用TDA近似的，原理上不如完整形式的TDDFT精确（详见《乱谈激发态的计算方法》http://sobereva.com/265），因此用tda false要求ORCA做完整形式的TDDFT计算。nroots 5代表计算5个激发态，当使用dosoc true的时候会自动用triplets true选项，因此会同时计算5个单重态激发态和5个三重态激发态。printlevel 3代表在SOC-TDDFT计算过程中比默认时输出更多信息，其中有很多是很重要的，而在默认下居然没有输出！（这点在手册只字未提，笔者好不容易才意外地试出来这个关键性的隐藏选项，简直像发现游戏秘技一样）。

计算开始后，程序按照以下流程计算和输出
(1)做常规B3LYP/TZVP基态计算以得到参考态波函数
(2)做常规TD-B3LYP/TZVP计算，先计算5个单重态激发态，再计算5个三重态激发态
(3)计算旋轨耦合积分，构建所有态之间的旋轨耦合矩阵元，然后对此矩阵对角化得到本征值和本征矢
(4)输出完整的旋轨耦合矩阵，实部和虚部分别输出，每个三重态当做不同的三个子态考虑
(5)输出单-三重态间旋轨耦合矩阵元
对于当前例子，其实算到这里就够了，后面几步的意义在之后的例子再细说。
(6)输出旋轨耦合对基态的稳定化能，即SOC stabilization of the ground state:后面的
(7)输出考虑了SOC后哈密顿的本征值，开头是Eigenvalues of the SOC matrix:
(8)输出考虑了SOC后哈密顿的本征矢，开头是Eigenvectors of the SOC matrix:
(9)输出不考虑SOC时的激发能、振子强度、转子强度、跃迁偶极矩等跃迁信息，标题为TD-DFT-EXCITATION SPECTRA
(10)输出考虑了SOC时的跃迁信息，标题为SOC CORRECTED TD-DFT/TDA-EXCITATION SPECTRA
此后还有些信息，就不是本文关注的了。

如果你用了printlevel 4，还会再额外输出基函数间的SOC积分、MO之间的SOC积分等信息，一般没必要输出这些，除非自己想基于这些数据写额外的程序。

具体来说，上述第(5)步依次输出以下四个矩阵
(a)各个单重态与各个三重态间的SOC算符的x,y,z三个分量对应的旋轨耦合矩阵元
(b)各个单重态与各个三重态的三个子态间的总旋轨耦合矩阵元
(c)各个单重态与各个三重态间的LxSx、LySy、LzSz算符（即简化的旋轨耦合算符）对应的旋轨耦合矩阵元
(d)各个三重态间的简化的旋轨耦合算符对应的旋轨耦合矩阵元

我们一般最关心的信息是上面(b)部分，也正是PySOC程序最终输出的，此例结果如下所示（如果不用printlevel 3，这个矩阵是不输出的）
                      CALCULATED SOCME BETWEEN TRIPLETS AND SINGLETS
      --------------------------------------------------------------------------------
           Root                          <T|HSO|S> (Re, Im) cm-1
         T      S           MS= 0                  -1                    +1
      --------------------------------------------------------------------------------
         1      0    (   0.00 , -63.78)    ( -0.00 ,    0.00)    ( -0.00 ,   -0.00)
         1      1    (   0.00 ,    0.00)    ( -0.00 ,   -0.00)    ( -0.00 ,    0.00)
         1      2    (   0.00 ,    0.00)    (   5.62 ,    0.00)    (   5.62 ,   -0.00)
         1      3    (   0.00 ,   -0.00)    ( -3.80 ,    0.00)    ( -3.80 ,   -0.00)
         1      4    (   0.00 ,   -0.00)    ( -0.00 , -38.41)    ( -0.00 ,   38.41)
         1      5    (   0.00 ,   45.07)    ( -0.00 ,   -0.00)    ( -0.00 ,    0.00)
         2      0    (   0.00 ,   -0.00)    (   0.00 ,   -0.00)    (   0.00 ,    0.00)
         2      1    (   0.00 ,   48.56)    (   0.00 ,    0.00)    (   0.00 ,   -0.00)
         2      2    (   0.00 ,    0.00)    (   0.00 ,   -0.30)    (   0.00 ,    0.30)
         2      3    (   0.00 ,    0.00)    (   0.00 ,    0.19)    (   0.00 ,   -0.19)
...[略]
S=0对应基态，S=1~5和T=1~5是算出来的5个单重态激发态和5个三重态激发态。MS=0、-1、+1对应三重态的自旋量子数不同的三个子态。可见ORCA对实部Re和虚部Im是分别输出的，而PySOC在输出的时候输出的是模，即实部和虚部平方和开根号。如果你想得到某个单重态和某个三重态之间总的旋轨耦合矩阵元，那就把这个单重态与三个子态的旋轨耦合矩阵元的模求平方再开根号，换句话说，就相当于把相应那一行的六个值都求平方加和后再开根号。根据上面的输出，我们可知诸如S1-T2之间的总旋轨耦合矩阵元是48.56 cm-1。

默认情况下，ORCA是以SOMF方式考虑旋轨耦合效应的，在ORCA里也被叫做SOMF(1X)。SOMF全称为Spin-orbit mean-field，它将SOC算符中难算的双电子部分用平均场方式来近似描述，精度比较理想，虽然名义上比起更粗糙的Zeff处理耗时高，但根据笔者测试，即便对于大体系的SOC-TDDFT计算，SOMF也不算耗时有多高，而且总耗时的瓶颈也完全不在计算旋轨耦合积分上。因此若无特殊情况，一律用默认的SOMF即可。

如果你就是想在SOC-TDDFT计算中用Zeff方式考虑旋轨耦合的话，在上面的输入文件中额外插入一行%rel SOCType 1 end即可（别写到%tddft...end里头去），这里%rel是设置旋轨耦合算符具体类型的段落。此时，在旋轨耦合部分计算开始处会看到
Operator type                               ... Effective nuclear charge
Effective nuclear charges used:
   Atomtype H -> Zeff     1.0000
   Atomtype C -> Zeff     3.6000
   Atomtype O -> Zeff     5.6000
这里用的ORCA内置的有效核电荷来自Koseki的文章，和笔者之前在http://sobereva.com/411中提到的一致。此时输出的旋轨耦合矩阵元为
           Root                          <T|HSO|S> (Re, Im) cm-1
         T      S           MS= 0                  -1                    +1
      --------------------------------------------------------------------------------
...[略]
         2      0    (   0.00 ,   -0.00)    (   0.00 ,   -0.00)    (   0.00 ,    0.00)
         2      1    (   0.00 ,   53.39)    (   0.00 ,    0.00)    (   0.00 ,   -0.00)
         2      2    (   0.00 ,    0.00)    (   0.00 ,   -0.33)    (   0.00 ,    0.33)
...[略]
此时<S1|H_SO|T2>为53.39 cm-1，和SOMF的结果48.56 cm-1稍有差异。如http://sobereva.com/411所示，之前用Gaussian+PySOC在相同级别下、结合Koseki有效核电荷时得到的这个值为49.81 cm-1，和此处的53.39 cm-1间的一点差异在于整个计算中涉及的各种零零碎碎的数值细节有所不同，而且PySOC计算时用的是笛卡尔型高斯函数，而当前是球谐型（ORCA里也只能用球谐型高斯函数）。

在ORCA里如果利用RI近似的话，对于大体系的基态和TDDFT计算都可以显著加快。由于甲醛很小，RI的效果不明显，甚至反倒令耗时更高，所以前例就没开RI。而对大体系，强烈建议把前例的关键词改为下面的关键词来节约时间
! B3LYP/G TZVP RIJCOSX def2/J miniprint tightSCF grid4 gridx4 pal4
RIJCOSX代表用RI-J加速库仑部分的计算，用COSX方法快速计算交换部分，gridx4代表用比默认更好的做COSX部分的积分格点以保证数值精度损失小。def2/J代表在RI-J部分使用def2/J辅助基组（def2/J辅助基组给def-系列基组用完全没问题）。对当前体系，开不开RIJCOSX对算出来的旋轨耦合矩阵元的绝对值影响不超过0.1 cm-1，所以SOC-TDDFT计算中可以放心用RIJCOSX来加速。更多RI相关的信息在《大体系弱相互作用计算的解决之道》（http://sobereva.com/214）一文有介绍。

3 旋轨耦合矩阵元计算实例2：溶剂中的Os配合物

在前述的《使用Gaussian+PySOC在TDDFT下计算旋轨耦合矩阵元》一文中用Gaussian+PySOC计算过下面这个Os配合物体系，基态是单重态

由于有重金属，因此我们一般都会想到用赝势基组，比同等质量的全电子基组又省时间又能顺带体现标量相对论效应。如果用Zeff方式考虑旋轨耦合的话，是可以使用赝势的。虽然如笔者的PySOC那篇博文所述，Koseki提出过适合Os等重元素的有效核电荷，结果也不差，但是ORCA 4.1.1里没有内置重元素的Koseki有效核电荷，虽然手册里说可以由用户自行提供，但笔者发现ORCA 4.1.1存在bug，按照手册里的方式自行提供了也会被程序无视。这点估计以后版本会修正，笔者已经在ORCA论坛反馈过了(https://orcaforum.kofo.mpg.de/viewtopic.php?f=8&t=4478)。因此，对此体系，时下我们只能用SOMF方式考虑旋轨耦合（ORCA还支持其几种变体，大同小异），此时只能用全电子基组，用赝势基组+赝势的话虽然不报错，但结果是明显不对的。

这次我们用以下关键词通过DKH2哈密顿来做全电子标量相对论计算，旋轨耦合只体现在TDDFT部分。完整的输入文件见本文的文件包。此任务用的几何结构和之前PySOC博文里相同。
! B3LYP/G DKH2 DKH-def2-TZVP SARC/J RIJCOSX cpcm(CH2Cl2) tightSCF miniprint grid4 gridx4
%basis
NewGTO Os "SARC-DKH-TZVP" end
end
%pal nprocs 36 end
%maxcore 2500
%tddft nroots=10 TDA false dosoc true printlevel 3 end
* xyz 0 1
...[坐标]
end
其中，DKH2代表用流行的DKH2哈密顿做标量相对论计算，基组使用DKH-def2-TZVP，是专为DKH计算设计的重收缩版本的def2-TZVP。由于def2-TZVP对于Os是赝势基组，所以DKH-def2-TZVP对Os必然是没有定义的，故此例对Os元素使用SARC-DKH-TZVP，此基组是对Xe之后元素有定义的适合DKH2计算的全电子基组，与DKH-def2-TZVP搭配很适合。虽然SARC/J名字看上去好像只是给SARC-DKH-系列基组用的辅助基组，但在ORCA里它也同时具有def2/J DecontractAuxJ（对def2/J辅助基组去收缩）的含义，因此无论是SARC-DKH系列（也包括SARC2-DKH）还是DKH-def2-系列基组都可以通过写SARC/J来提供适合的辅助基组。当前计算使用CPCM模型表现二氯甲烷CH2Cl2溶剂环境。由于当前计算较耗时，故用36个核计算，每个核内存分配上限约为2500MB。

当前这个任务，在http://bbs.keinsci.com/thread-6310-1-1.html一文提到的笔者买的E5-2696 v3双路36核机子下只花了12分钟就跑完了。旋轨耦合矩阵元部分输出如下
           Root                          <T|HSO|S> (Re, Im) cm-1
         T      S           MS= 0                  -1                    +1
      --------------------------------------------------------------------------------
         1      0    (   0.00 ,    0.01)    ( -59.62 ,    7.55)    ( -59.62 ,   -7.55)
         1      1    (   0.00 ,   89.52)    (   0.03 ,    0.00)    (   0.03 ,   -0.00)
...[略]
         1      9    (   0.00 ,    3.58)    (   0.04 ,    0.05)    (   0.04 ,   -0.05)
         1     10    (   0.00 ,    0.03)    (   1.48 , -40.59)    (   1.48 ,   40.59)
         2      0    (   0.00 , -198.63)    ( -0.86 ,    0.23)    ( -0.86 ,   -0.23)
         2      1    (   0.00 ,   -1.30)    (-544.99 ,   16.42)    (-544.99 , -16.42)
         2      2    (   0.00 ,    0.94)    ( -70.51 , 665.08)    ( -70.51 , -665.08)
...[略]
比如<S1|H_SO|T2>的总大小为sqrt((-1.30)**2+(-544.99)**2+16.42**2+(-544.99)**2+(-16.42)**2)=771.1 cm-1。之前PySOC那篇博文里，用Gaussian+PySOC通过TD-B3LYP/def2-TZVP结合IEFPCM溶剂模型得到的结果为<S1|H_SO|T2_0>=0.69 cm-1、<S1|H_SO|T2_+1>=<S1|H_SO|T2_-1>=419.63 cm-1，总大小593.4 cm-1，和当前算的结果数量级差不多。由于当前计算明显更为严格，又是用全电子标量相对论又是用更好的SOMF方式考虑旋轨耦合，特别是Zeff方法对于越重的元素往往误差越大，因此应当认为本文的结果更合理。

关于ORCA在溶剂模型下输出的TDDFT激发能有一些特殊问题值得提及。在输出完三重态激发能之后，有这么一段（这里State 0是指的第1个三重态激发态）
State Shift(Eh) Shift(eV) Shift(cm**-1) Shift(nm) ERPA(eV) ERPA+SHIFT(eV)
-------------------------------------------------------------------
   0: -0.0006565 -0.018     -144.1        3.5      2.534     2.516
   1: -0.0120876 -0.329    -2652.9       28.4      3.954     3.626
   2: -0.0100690 -0.274    -2209.9       22.6      4.012     3.738
   3: -0.0011292 -0.031     -247.8        2.1      4.287     4.256
   4: -0.0024908 -0.068     -546.7        4.6      4.330     4.262
   5: -0.0021236 -0.058     -466.1        3.8      4.365     4.307
   6: -0.0297932 -0.811    -6538.8       61.7      4.461     3.650
   7: -0.0083835 -0.228    -1840.0       14.9      4.475     4.247
   8: -0.0007398 -0.020     -162.4        1.2      4.486     4.466
   9: -0.0003368 -0.009      -73.9        0.5      4.569     4.560
我在《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》（http://sobereva.com/314）中说过，溶剂对电子激发的响应有快部分和慢部分之分，两部分都会影响激发能。上面的ERPA下面的数值对应的只是只考虑了慢部分的情况，相当于是用溶剂模型下经过SCF得到的基态轨道以常规方式算的TDDFT激发能，ORCA是根据这个激发能来对激发态进行排序的。Shift是溶剂的快部分对激发能的影响，体现的是对电子激发的瞬时响应，二者的加和ERPA+SHIFT也正是在这个表格之前输出的各个激发态的能量，它和ERPA的顺序可能存在不同。而Gaussian则是按照最终的（快、慢部分都考虑后的）激发能对激发态来排序的。因此由于这个差异，Gaussian与ORCA给出的激发态顺序可能不同。

另外，Gaussian与ORCA虽然在气相下算的TDDFT激发能相符很好，但在溶剂模型下则有很大出入（对于电子激发，ORCA只能用线性响应溶剂模型，而这里作为对比的对象是Gaussian也用线性响应溶剂模型的情况）。这俩程序都用CPCM时，由于用的默认原子半径不同等细节因素存在差异，结果肯定是对应不好的，这暂且不提；哪怕这两个程序都用SMD溶剂模型，让溶剂方面的细节尽可能一致（仍不完全相同，因为ORCA的SMD的极性部分不是用的SMD原文里的IEFPCM而是更low的CPCM形式），这俩程序给出的某些态的TDDFT激发能也是存在明显不同的（已经通过组态系数可以确认对比的是相同的态），相差往往达到零点几eV的程度。根据笔者的感觉，ORCA算出来的溶剂的快部分是不太可靠的，即SHIFT数值往往太大，如上可见有的居然能达到-0.8 eV的程度，更何况当前用的二氯甲烷极性很低，不可能会产生这么大影响才对。而由于Gaussian在溶剂模型方面有资历深厚的专家Barone等人在做，发表过很多关于溶剂效应对电子激发问题的理论文章，因此我认为Gaussian的结果明显更可信。而且，如果不考虑快部分，即直接用ORCA输出的ERPA的结果与Gaussian给出的结果相比，则能基本相符，进一步体现ORCA给出的快部分应当是有严重问题的。

根据以上讨论，对于溶剂模型下ORCA给出的SOC-TDDFT旋轨耦合矩阵元，就用直接输出的态的编号讨论就行了，而不建议根据实际输出的激发能（也等同于上表中的ERPA+SHIFT）再对激发态手动重新排序。如上可见，重新排序的话有的态的序号会有明显改变，比如从上面的表里看到ORCA给出的第7个三重态激发态的最终的激发能是3.650 eV，如果按照最终激发能来重新排序的话，它就成了T3而非T7了。

4 旋轨耦合校正后的UV-Vis光谱的绘制实例：Ir(bzq)2(acac)配合物

普通TDDFT计算时，由于自旋禁阻，单重态基态与三重态激发态之间的振子强度精确为0，而考虑旋轨耦合后，就不再如此。ORCA的SOC-TDDFT任务会输出在TDDFT过程中考虑旋轨耦合后基态到各个激发态的激发能和振子强度。具体是这么做的：先构建基态以及所有激发态之间的旋轨耦合矩阵元并加到原本的哈密顿矩阵上，每个三重态当做不同的三个子态来考虑。然后对这个矩阵做对角化，这等同于以原先的单、三重态电子态波函数作为基在考虑了旋轨耦合算符的哈密顿下做变分。这样得到的每个本征矢就相当于是考虑了旋轨耦合后的每个电子态的波函数，形式上是原先各个单重态电子态和三重态电子态的线性组合，组合系数就是这个本征矢的相应元素，而本征值就对应于考虑旋轨耦合后各个电子态的能量。此时，基态与激发态之间就不再自旋禁阻了，因为基态和激发态现在都同时具有单、三重态的成份，不再是S^2算符的本征函数，因此去计算基态与激发态之间的跃迁偶极矩时，其中不仅包含原本因为自旋禁阻而精确为0的<S|-r|T>项，还包括可以不为零的<S|-r|S>和<T|-r|T>项。另外，新产生的电子态的能量显然和之前电子态的能量不同，无论对于基态还是激发态都是如此。新的基态与原先基态之间的能量变化就是ORCA输出的SOC stabilization of the ground state。PS：由于ORCA的SOC-TDDFT在撰文时还没有相关文章发表，所以上叙述只是来自笔者个人的判断。

看过不少磷光速率计算的读者应该也知道，还有一种常见的得到单-三重态间振子强度的方法是使用一阶微扰理论，也就是将旋轨耦合算符作为微扰项来修正原有的波函数，经由S-T间的SOC矩阵元使三重态掺入单重态，也让单重态掺入三重态，这样最终得到的S-T混合态之间的跃迁偶极矩就可以不为零了，因此振子强度也就可以不为零了。从原理上说，ORCA用的变分方式的处理应当更为严格，因为相当于可以考虑更高阶的混合效应，而且可以顺带直接给出考虑SOC后的电子态的能量，但需要额外付出的代价是还得计算三重态激发态之间的旋轨耦合矩阵元，这占了整个旋轨耦合矩阵的大部分。

基于考虑旋轨耦合后产生的新的态的激发能和振子强度、转子强度，原理上就可以照常绘制UV-Vis光谱和ECD光谱了。但遗憾的是，目前的ORCA 4.1.1在SOC-TDDFT计算过程中给出的考虑旋轨耦合后的激发态的转子强度是错的。在考虑SOC前输出的有正有负，是合理的，但是考虑SOC后全都成正的了，明显不对，因此绘制出来的ECD光谱也无意义。这个问题我已经在ORCA论坛进行了反馈（https://orcaforum.kofo.mpg.de/viewtopic.php?f=8&t=4479），Neese说这应该是bug，但愿在未来版本中会修正。

下面笔者以下图这个Ir(bzq)2(acac)体系作为例子演示绘制旋轨耦合校正后的UV-Vis光谱。

这里使用下面的关键词算对Ir(bzq)2(acac)进行计算，体系基态是单重态。
! B3LYP/G DKH2 DKH-def2-TZVP(-f) SARC/J RIJCOSX tightSCF miniprint grid4 gridx4
%pal nprocs 36 end
%maxcore 2500
%basis
NewGTO Ir "SARC-DKH-TZVP" end
end
%tddft nroots=100 TDA false dosoc true printlevel 3 end
# BP86/SDD/TZVP opted
* xyz 0 1
...[坐标]
end
其中#开头的行是注释行，后面的内容用于提示自己之前这个结构是在BP86结合SDD和def-TZVP基组优化后的。DKH-def2-TZVP(-f)代表把DKH-def2-TZVP基组中的f极化函数砍掉以节约时间。如《谈谈赝势基组的选用》（http://sobereva.com/373）里提过的，配体的地位没有处于体系中央的过渡金属高，再加上普通泛函对高角动量函数要求比较低，因此用-f的版本不至于令误差比不带-f的版本增加太多。顺带一提，ORCA的SCF收敛做得不如Gaussian好，当前这样的关键词算某些过渡金属配合物容易遇到SCF不收敛，碰见这种情况可以尝试加上slowconv或veryslowconv关键词，此时会用对一般情况来说更慢但是更稳妥、收敛成功几率更高的收敛设定和算法，实测挺奏效。当前例子我们要算的并不是S与T不同子态间的旋轨耦合矩阵元，因此printlevel 3其实可以去掉，此时由于可以少输出许多矩阵，输出文件会小很多。当前这个任务用2*E5-2696 v3的机子在36核并行时4h13m算完。

Multiwfn是绘制各种类型电子和振动光谱的又方便又强大的程序，可在http://sobereva.com/multiwfn下载。相关信息看《Multiwfn入门tips》（http://sobereva.com/167）。在《使用Multiwfn绘制红外、拉曼、UV-Vis、ECD、VCD和ROA光谱图》（http://sobereva.com/224）中对各种光谱的计算和绘制原理以及在Multiwfn中的操作都有详细说明。2019年1月22日之后更新的Multiwfn支持基于Multiwfn的SOC-TDDFT计算的输出文件绘制UV-Vis和ECD谱。

启动Multiwfn，输入上面计算产生的输出文件的路径，然后依次输入
11 //绘制光谱
3 //UV-Vis
y //载入考虑了SOC之后的电子激发数据。如果选n则载入的是考虑SOC之前的
0 //绘制光谱，显示到屏幕上
此时屏幕会立刻看到图像。为了美观，我们调整一下坐标轴范围和标签间隔。关闭窗口，继续输入
3 //设置横坐标
150,550,50 //范围为150~550nm，间隔50nm
4 //设置左侧坐标轴
0,60000,5000
y //让右侧坐标轴同步调节
此时再选0，看到的图像如下

我们也可以将考虑SOC和不考虑时候的图绘制到一起，便于考察SOC对光谱的影响。这用Multiwfn非常容易实现，怎么用Multiwfn绘制多个情况下的光谱在《使用Multiwfn绘制构象权重平均的光谱》（http://sobereva.com/383）一文末尾明确说过。创建一个名为multiple.txt的文件，内容如下（.out路径写的是实际路径），第一部分是文件名，之后是要显示在图上的图例。
E:\Ir_bzq2_acac.out with SOC
E:\Ir_bzq2_acac.out without SOC
然后启动Multiwfn，载入multiple.txt，重复一遍上面绘制UV-Vis光谱的过程。与上例唯一不同的是载入文件的时候会载入两次Ir_bzq2_acac.out，第一次问你是否载入SOC校正后的光谱信息时输入y，第二次问你的时候输入n（注意，由于考虑SOC后每个三重态作为三个不同的态考虑，态数比不考虑SOC时要多，而Multiwfn里同时绘制多个光谱时要求态数最多的情况作为第一项出现，因此multiple.txt里必须第一条对应的是SOC的情况）。绘制的结果如下：

由图可见，SOC效应使得UV-Vis光谱整体蓝移几十nm。按理说，肯定是考虑SOC之后的光谱更合理，但对于这点，笔者持保留态度。因为对于过渡金属配合物的计算，只要计算级别合理，其实不考虑SOC就已经可以算得很不错了，而ORCA这样考虑SOC后，对结果影响却如此之大，所以可能结果变得更差。笔者手头没有此体系的实验光谱，而且即便有，也有可能因为与其它因素带来的误差的侥幸抵消而妨碍判断，所以考虑SOC后光谱是否更合理这点笔者在此文就暂不深究了。读者有兴趣的话可以考虑和免费的专做相对论计算的Dirac程序做的二分量TDDFT计算得到的光谱对照一下，以看看ORCA这种SOC的考虑是否对改进TDDFT光谱确实有益。

这里再提一下当前体系考虑SOC后的激发能具体怎么来的。ORCA计算三重态时输出的原始的T1激发能是
STATE 1: E=   0.082507 au      2.245 eV    18108.3 cm**-1
   155a -> 159a :     0.047168
   156a -> 159a :     0.030710
   157a -> 158a :     0.873592
在SOC矩阵构造完毕并对角化考虑了SOC的哈密顿矩阵后，输出了如下信息
SOC stabilization of the ground state: -1692.8499 cm-1
Eigenvalues of the SOC matrix:

   State:        cm-1         eV
     0:          0.00         0.0000
     1:      19166.96         2.3764
     2:      19201.28         2.3807
     3:      19269.86         2.3892
     4:      19499.20         2.4176
...略
可见此处输出的State 1,2,3的激发能比较接近，这三个态实际上就是T1态分裂出的三个子态。原先T1的激发能是18108.3 cm-1左右，考虑SOC后分裂出的三个态激发能是19200 cm-1左右，明显高了不少。但是这还不是最终的激发能，因为前面提示了，SOC还导致基态能量下降了-1692.8499 cm-1，因此T1最低的那个子态最终的激发能是19166.96+1692.85=20859.8 cm-1，这和我们在靠后部分看到的输出考虑SOC后的激发能、振子强度和跃迁偶极矩的段落中的信息是一致的
-----------------------------------------------------------------------------
SOC CORRECTED ABSORPTION SPECTRUM VIA TRANSITION ELECTRIC DIPOLE MOMENTS*
-----------------------------------------------------------------------------
State   Energy Wavelength   fosc         T2         TX        TY        TZ
        (cm-1)    (nm)                  (au**2)     (au)      (au)      (au)
-----------------------------------------------------------------------------
   1   20859.8    479.4   0.000051143   0.00081   0.02788   0.00000   0.00548
...略
正是因为此例中SOC既提升了激发态能量又降低了基态能量，因此使得光谱整体出现了明显蓝移。

关于算的态数这里多说几句。由于当前体系较大，对于绘制电子光谱目的，计算的态数不能太少，像之前计算Os配合物那样只算10个态是绝对不够的，最少也得算50个态。下图是Multiwfn绘制的不考虑旋轨耦合时计算50、100、150个态的对比图（为节约耗时，配体用的是DKH-def2-SV(P)），可见至少算50个态的时候300nm以上的曲线才能保证真实、完整。

ORCA考虑SOC对光谱的影响靠的是让不考虑SOC时得到的单重态和三重态混合来实现的，只有当算的态数比较多时，也相当于令“基”完备性较高时，考虑SOC后的电子态才能被较好描述，这样得到的考虑SOC后的激发态的振子强度和激发能才可能比较合理。在绘制SOC下的UV-Vis光谱时，算的态数应当比起不考虑SOC时更多。下图是计算50、100、150个态的时候在考虑SOC后的对比图

我们就关注300nm右侧的区域就够了。由图可见，算50个态和算100个态的时候光谱曲线是有明显可察觉的差异的，而计算100个态和计算150个态的光谱则看不出太大差异。如果不考虑SOC，如之前的图可见，算50、100还是150个态在300nm以上区域是肉眼完全看不出差异的。这个现象说明，在考虑SOC时，只计算50个态还不足以令光谱达到收敛，计算100个态的时候则基本达到收敛了。像此例类似的体系，做SOC-TDDFT计算光谱时，我都建议计算不少于100个态以求稳妥。

随着计算的态数增加，SOC-TDDFT耗时也会迅速增加，所以也不能盲目算得太多。当算的态数很多时，最最耗时的步骤就是构建完整的SOC矩阵。对本例的体系，在B3LYP下对配体用DKH-def2-SV(P)、Ir用SARC-DKH-TZVP，在前述36核机子下以SOC-TDDFT方式算50、100、150个态的耗时分别为27m、79m、169m。值得一提的是，虽然ORCA默认用的SOMF(1X)方式考虑旋轨耦合比Zeff要贵，但是对于计算的态数较多时，其实总耗时都差不多，因为瓶颈完全不在于计算旋轨耦合积分的部分。

5 基于ORCA的SOC-TDDFT输出信息计算磷光发射速率靠谱么？

磷光发射对应T1->S0，因此，如果找出T1主要对应的在考虑旋轨耦合后产生的三个态的振子强度和激发能，我们还可以计算磷光发射速率。在《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》（http://sobereva.com/314）中说过自发辐射速率怎么算。对于T1的一个子态，只要把其激发能、振子强度都代进去，就可以得到从这个子态发磷光的速率。要算总的磷光速率，图省事可以直接把三个子态的发射速率取平均，但原理上更严格的方法是将三个子态的发射速率取权重平均，权重可以通过Boltzmann分布获得，见《根据Boltzmann分布计算分子不同构象所占比例》（http://sobereva.com/165），只不过此时公式里的各个构象相对于最稳定构象的自由能差应该改为各个子态相对于能量最低子态的激发能差。

基于ORCA的SOC-TDDFT输出的信息按上述方式算磷光发射速率的结果靠谱么？我们还用上一节Ir(bzq)2(acac)那个例子，看看算出的结果和实验值相符如何。我们从输出文件中找到下面部分
SOC CORRECTED ABSORPTION SPECTRUM VIA TRANSITION ELECTRIC DIPOLE MOMENTS*
-----------------------------------------------------------------------------
State   Energy Wavelength   fosc         T2         TX        TY        TZ
        (cm-1)    (nm)                  (au**2)     (au)      (au)      (au)
-----------------------------------------------------------------------------
   1   20859.8    479.4   0.000051143   0.00081   0.02788   0.00000   0.00548
   2   20894.1    478.6   0.000053714   0.00085   0.00007   0.02909   0.00002
   3   20962.7    477.0   0.002733492   0.04293   0.20278   0.00003   0.04251
   4   21192.1    471.9   0.000006626   0.00010   0.00001   0.01015   0.00000
   5   21260.4    470.4   0.002483201   0.03845   0.19479   0.00011   0.02259
   6   21273.4    470.1   0.000053372   0.00083   0.00093   0.02872   0.00012
...略

由于T1的能量低于其它激发态，而且从以上信息看，前三个态的激发能很接近（旋轨耦合造成的能量分裂程度一般不会很大），因此可以初步认为前三个态就是T1分裂出的子态。但由于S1可能与T1能量较为接近，所以光从能量上判断哪三个态对应原始的T1也不是绝对稳妥的。我们可以考察下考虑SOC后的哈密顿矩阵对角化产生的本征矢的构成来进一步判断。从输出文件中可以找到下面信息
Eigenvectors of the SOC matrix:

             E(cm-1) Weight      Real         Imag     : Root Spin Ms
STATE 0:      0.00
                      0.95663     -0.97807     -0.00121 : 0     0     0
STATE 1: 19166.96
                      0.45282      0.67290      0.00545 : 1     1     0
                      0.01878     -0.13705     -0.00111 : 4     1     0
                      0.19397      0.44040      0.00356 : 1     1    -1
                      0.03062     -0.00138      0.17499 : 3     1    -1
                      0.01131      0.00079     -0.10635 : 5     1    -1
                      0.19397     -0.44040     -0.00357 : 1     1     1
                      0.03062     -0.00145      0.17499 : 3     1     1
                      0.01131      0.00094     -0.10635 : 5     1     1
STATE 2: 19201.28
                      0.03764      0.00211      0.19399 : 3     1     0
                      0.40524      0.63655     -0.00725 : 1     1    -1
                      0.01383     -0.00127     -0.11758 : 2     1    -1
                      0.02012      0.00149      0.14183 : 3     1    -1
                      0.40524      0.63655     -0.00661 : 1     1     1
                      0.01383      0.00129      0.11758 : 2     1     1
                      0.02012     -0.00159     -0.14183 : 3     1     1
STATE 3: 19269.86
                      0.01172      0.00207     -0.10824 : 2     0     0
                      0.03248      0.00345     -0.18018 : 3     0     0
                      0.39122      0.62536      0.01197 : 1     1     0
                      0.23609     -0.48581     -0.00888 : 1     1    -1
                      0.01004      0.00202     -0.10017 : 2     1    -1
                      0.01122      0.10591      0.00201 : 4     1    -1
                      0.23609      0.48579      0.00972 : 1     1     1
                      0.01004      0.00182     -0.10018 : 2     1     1
                      0.01122     -0.10590     -0.00205 : 4     1     1
...略（注意给出的能量是没有加上SOC导致的基态稳定化能的）

上面的信息展现了考虑SOC后新产生的电子态是怎么由原先的各个单重态和三重态混合产生的，Weight下面是贡献，总和为1（这里只输出了>0.01的）。Root下面是不考虑SOC时电子态的序号，0是基态，Spin为0和1分别对应单重态和三重态。

由以上信息可见，考虑SOC后能量最低的三个激发态几乎完全由三重态构成，而且原先的T1（Root=1,Spin=1的项）起到的贡献是最主要的。毫无疑问考虑SOC后得到的激发能最低的三个态一起对应了T1，用这三个态的信息，从原理上就可以计算磷光发射速率。

笔者做了一个Excel表格，把T1的三个子态的激发能和振子强度输进去，就可以计算各个子态的发射速率、寿命以及Boltzmann分布比率，在表格最下面给出算术平均和权重平均后的发射速率。对当前情况，结果如下所示

在J. Phys. Chem. C, 117, 25714 (2013)中给出了此体系的实验磷光速率，是0.6E-5 /s，明显比我们算出来的209869.5 /s低得多，连数量级都不对应！虽说实验值是在2-MeTHF下测的，但溶剂效应也不会导致这么大差异，比如在CH2Cl2下算的此体系的权重平均的磷光速率是182851.2 /s，也没比当前气相算出来的小太多。当前虽然我们用的结构是基态优化的，而计算磷光理应使用对T1态优化的结构，但结构的这点差异也不会导致算出来的磷光速率产生数量级的差异（而且JPCC这篇文章提到有人发现用基态优化的结构算磷光反倒更准，且认为由于T1极小点的势阱很浅，因此实际磷光发射的结构介于S0和T1结构之间，故这篇文章都用S0结构算的）。总之，基于ORCA的SOC-TDDFT输出的数据，用常规计算磷光速率的方式，结果是很不可靠的（虽然我也发现对于个别配合物体系如Ir(ppy)3的结果基本合理，但终究稳健程度低，不敢用）。而且为了令SOC效应考虑充分，还不得不算很多态，起码100个（最好还做个结果随态数增加的收敛性测试），此时耗时也较高，所以大家就别指望利用ORCA以上述方式算磷光速率了。

顺带一提，Dalton算是目前最理想的算磷光速率的程序，而且免费，它算磷光速率是基于响应函数理论算的，等同于算无穷数目激发态，因此原理上更高级。之前笔者对此体系，用Dalton2016，以Zeff方式考虑旋轨耦合，在TD-B3LYP/6-31G*/SDD下算的结果是6.2E4 /s，和实验相符奇好（当然很大程度上是巧合），用2*E5-2696v3 36核机子只花了一个小时。以后有时间我会专门撰文简要介绍怎么用Dalton实现磷光速率的计算，在北京科音高级量子化学培训班里会更深入地讲。

↧

量子化学程序Dalton的编译方法和运行方式简介

February 10, 2019, 11:39 pm

≫ Next: 2018年下半年观看的非TV版动画简评

≪ Previous: 使用ORCA在TDDFT下计算旋轨耦合矩阵元和绘制旋轨耦合校正的UV-Vis光谱

量子化学程序Dalton的编译方法和运行方式简介

文/Sobereva@北京科音 2019-Feb-11

开源免费的量子化学程序Dalton（http://daltonprogram.org）虽然用起来比较复杂，对新手很不友好，但由于其擅长计算响应性质，是其它程序难以取代的，所以它有着独特的地位。本文介绍怎么安装Dalton，也简单介绍一下怎么运行。本文说的Dalton都指的是Dalton suite中1983年开始发展的那个Dalton程序，而非Dalton suite中从Dalton分化出来的线性标度版Dalton（LSDalton）。

1 Dalton的编译

下文的安装过程对于Dalton2018.1是适用的，对最新或更老版本不一定适用。笔者的操作系统为CentOS 7.2 64bit，CentOS是最适合计算服务器用的Linux操作系统，下文的编译过程对于其它系统不一定适用，请随机应变。笔者用的是root用户。

本文假定读者已经在机子里装了Intel Parallel Studio XE 2019 Update 1中的Intel Fortran编译器、Intel C/C++编译器、Intel MKL数学库和Intel MPI库。如果不会装的话，参看《VASP最简单的安装方法》（http://sobereva.com/455）里的说明和视频演示，本文不再累述。
PS：原则上，Dalton用gfortran/gcc+OpenMPI也可以编译，但不建议如此，毕竟这样编译出的代码比用ifort/icc慢，而且笔者发现起码对于2019-Feb-10下载的最新的Dalton，gfortran由于与个别文件的语法兼容性问题编译不过去。

1.1 安装cmake 3.x

如果在你用的系统里输入cmake --version显示的是3.x版本，而且编译Dalton的过程没有提示cmake版本太低，那就可以略过此步。由于CentOS 7.2自带的cmake是2.8的，而Dalton 2018要求3.x版本，因此先得装更新的cmake。

在联网的情况下运行以下命令
yum install cmake3
mv /usr/bin/cmake /usr/bin/cmake2
ln -s /usr/bin/cmake3 /usr/bin/cmake
这里把自带的cmake 2.8备份为cmake2，而把新装的cmake3做了一个符号链接，这样试图调用cmake的程序就用的是cmake 3.x版了。

1.2 下载Dalton

在Linux的命令行下运行：
git clone --recursive https://gitlab.com/dalton/dalton.git
就会把最新版本Dalton下载到当前目录下作为dalton目录。这个“最新版本”体现了开发者迄今对dalton所做的所有最新的改动。然后手动将此目录改名为dalton_src。

注意，不要自行去https://gitlab.com/dalton/dalton点击download下载压缩包，因为Dalton的gitlab项目上的external目录的内容里包含外部project，直接下载的压缩包里面是没有那些project的文件的，只有用上面这种方式才能完整下载。之后你可以把这个下载的目录压缩后保留起来，便于以后用或者给其他人用。

1.3 编译Dalton的MPI并行版

Dalton主要是靠MPI并行的。由于当前机子里已经有了Intel MPI，所以就不用再额外装MPI库了。MPI版Dalton应当链接串行版MKL库，

下面的过程将把Dalton安装到/sob/dalton目录下。依次运行
cd dalton_src
./setup --fc=mpiifort --cc=mpiicc --cxx=mpiicpc --mkl=sequential --prefix=/sob
cd build
make install -j
Intel 36核机子下2分钟就编译完毕了。此时出现了/sob/dalton目录，里面包含了可执行文件和相关文件，总共占80MB左右。（在vmware虚拟机下用-j可能会在编译中途卡住，去掉-j以串行方式编译，得花大约半个小时）

把以下内容加入到用户目录下的.bashrc：
export PATH=$PATH:/sob/dalton
export DALTON_TMPDIR=/sob （之后临时文件默认都将产生在/sob/DALTON_scratch_root目录下）
export DALTON_LAUNCHER="mpirun -np 36" （-np后面设的是默认情况下运行用的并行进程数）
重新进入终端，以使以上语句生效。现在就可以通过输入dalton命令来运行了。

在dalton_src/build目录下运行ctest命令进行测试，Dalton 2018.1版总共约500个测试，在笔者的Intel 36核机子上并行执行总共花了不到半个小时。有些测试项目可能会提示Failed，但也别太担心，一般来说只要编译成功，出现Failed并不是编译有问题，而更可能是开发者提供的参考文件有问题或者测试项目本身有问题（比如有的功能不支持MPI并行），想一探究竟的话可以去Dalton的临时文件目录下找failed的项目的输出文件，看到底是怎么回事。

1.4 编译Dalton的串行+MKL并行版（以下简称MKL并行版）

Dalton的有些功能并不支持MPI并行，比如耦合簇计算功能。使用这些功能时如果你用的是MPI并行版Dalton，那并行进程数只能设为1，或者使用Dalton的串行版。由于Dalton所调用的Intel MKL数学库在运行的时候是支持OpenMP方式并行的，因此对于Dalton的不支持MPI并行的功能，你若在计算的时候想利用多核提升速度，可以编译Dalton的串行版但是链接并行版本的MKL库。下面来编译一下这种版本。

先把之前编译出来的Dalton MPI并行版的目录改个名免得被覆盖掉，比如叫dalton_MPI。然后进入dalton_src目录，把之前的build目录删掉，然后运行
./setup --fc=ifort --cc=icc --cxx=icpc --mkl=parallel --prefix=/sob
cd build
make install -j
在.bashrc里把export DALTON_LAUNCHER="mpirun -np 36"前面加上#注释掉，再加入export OMP_NUM_THREADS=36来让MKL库默认通过36线程并行，之后重新进入终端使设置生效。

通过MKL实现并行可以跑所有任务，而通过MPI实现并行只能跑支持MPI并行的任务。凡是能用MPI并行的任务建议用MPI并行版来跑，耗时一般比用MKL并行版更低，毕竟Dalton里调用MKL数学库的代码本身就是很有限的。

所有前述编译都完成，而且测试也都完成后，dalton_src目录就没用了，可以删了。另外值得提醒的是，时间长了可能在Dalton的临时文件目录里积攒很多老旧临时文件，记得时不时清一清。

2 Dalton的运行

2.1 运行格式

一般情况需要一个.dal文件，内含计算任务的说明；还需要一个.mol文件，内含分子结构、基组定义。

一般运行的格式：dalton [选项] [.dal] [.mol]
例如，dalton DFT1 H2O代表用DFT1.dal里定义的设置和任务去算H2O.mol里的体系。

运行完毕后在当前目录下的出现的"dal名_mol名.out"是输出文件（dal和mol名相同时只包含一次名字）。同时还产生同名的.tar.gz文件，这个压缩包内含运行期间输出的各种零碎文件，其中molden.inp就是.molden输入文件，可以用笔者开发的Multiwfn程序（http://sobereva.com/multiwfn）直接载入此文件做各种波函数分析、观看结构和轨道（主功能0）。相关常识看《Multiwfn入门tips》（http://sobereva.com/167）、《使用Multiwfn观看分子轨道》（http://sobereva.com/269）。

运算期间不会在屏幕上显示运算过程细节信息。如果运算期间要监控运算过程，可以随时查看这个文件的内容：$DALTON_TMPDIR/DALTON_scratch_用户名/dal名_mol名_pid号/DALTON.OUT。也可以用tail -f [文件名]的做法来实时把此文件里最新写入的信息同步输出到屏幕上便于监控。

2.2 常用选项

直接输入dalton命令就可以查看能够接的选项，这里说几个常用的。

-N 36：代表用36个MPI进程进行并行运算，仅对于MPI并行版Dalton有意义。如果没用此选项，就会用DALTON_LAUNCHER环境变量里设的核数来并行计算
-omp 36：代表通过MKL以OpenMP方式并行时用36个线程并行运算，仅对于MKL并行版有意义。如果没用此选项，就会用OMP_NUM_THREADS环境变量指定的线程数
-mb 1200：设定当前计算用1200MB内存。默认用的最大内存量也可以用WRKMEM环境变量来设，单位与此相同
-noarch：不让当前任务产生.tar.gz文件
-nobackup：不备份以前的输出文件。默认情况下如果之前有同名的输出文件存在，会在后面加上数字作为后缀来备份
-ow：计算过程产生的输出文件"dal名_mol名.out"直接输出到当前目录。默认情况下在运算过程中输出文件被输出到前述DALTON_TMPDIR定义的目录里，算完之后才自动挪到当前目录
-o [文件名]：直接指定输出文件名字，而且运算过程中就直接产生

Dalton运行时用的命令"dalton"实际上是dalton目录下面的一个bash脚本，用来设定运行环境，并调用实际可执行文件dalton.x。这类似于GAMESS的rungms脚本。如果想把一些选项设为默认的，可以在dalton脚本中修改70行开始的位置（此位置是对于Dalton 2018.1的而言）的一些参数。比如想把nobackup、noarch、ow作为默认启用的选项，就把opt_nobackup、opt_noarch都设为1，把opto设为2。稍微读一下此脚本就知道为什么这么设了。

如果MPI并行版和MKL并行版在平时研究中都用得着，MKL并行版放在了/sob/dalton目录，MPI并行版放在了/sob/dalton_MPI目录，为了能方便地同时使用，建议在.bashrc里既不设DALTON_LAUNCHER也不设OMP_NUM_THREADS，但是加一句alias daltonmpi='/sob/dalton_MPI/dalton'。此时就可以这样运行了：
36核跑MKL并行版：dalton -omp 36 love live
36核跑MPI并行版：daltonmpi -N 36 love live

2.3 输入文件简介与简单例子

首先注意几点：
Dalton对基组的大小写敏感，比如aug-cc-pVDZ不能写为aug-cc-pvdz。
Dalton主要用来计算闭壳层的基态，因此多数情况下并不需要给出自旋多重度，默认就是1。
Dalton默认对所有基组都用球谐函数。
Dalton默认是不冻核的。
.dal里可以用#或!进行注释。

下面是一个CCSD(T)单点计算的dal文件例子：
**DALTON INPUT     //**是主选项
.RUN WAVE FUNCTIONS   //.后面代表设定。RUN后面设的是要干什么、调用什么模块
**WAVE FUNCTIONS
.CC   //耦合簇波函数
*CC INPUT   //对CC计算进行进一步设定
.CC(T)
**END OF INPUT

下面是一个B3LYP下优化任务的dal文件例子。注意Dalton默认的B3LYP的定义与Gaussian不同，B3LYPg代表使用与Gaussian相同的定义：
**DALTON INPUT
.OPTIMIZE
**WAVE FUNCTIONS
.DFT
B3LYPg
**END OF INPUT

下面是一个甲酰胺的mol文件例子：
ATOMBASIS //代表每个原子分别设定基组。如果这里写BASIS，然后下面再加一行6-31G*，则说明所有原子都用这个基组，每类原子里的Basis=6-31G*就不要再写了
test molecule //标题行，内容任意，必须有
Generated by Multiwfn //同上
Atomtypes=4 Angstrom Nosymmetry charge=0 //关键词顺序随意，大小写敏感。可以只写前三个字符。当前设置说明体系里包含四类原子，坐标单位是埃，不用对称性，是电中性
Charge=1.0 Atoms=3 Basis=6-31G* //此类原子的实际核电荷数、原子数、基组
H1   -0.45438149    1.43099761    0.00000000   //原子名可随意定义，程序不检查
H2   -0.64184099   -1.52402451    0.00000000
H3   -1.92375124   -0.35013241    0.00000000
Charge=6.0 Atoms=1 Basis=6-31G*
C1    0.00000000    0.41905994    0.00000000
Charge=7.0 Atoms=1 Basis=6-31G*
N1   -0.94010085   -0.56081903    0.00000000
Charge=8.0 Atoms=1 Basis=6-31G*
O1    1.20008496    0.23181661    0.00000000

上面设的Atomtypes指的不是元素种类，而是原子类型。比如O3，是C2v点群，虽然只有一种元素，但是有两种非等价的氧，故Atomtypes=2。如果懒得考虑这个，直接用Nosymmetry，这样Atomtypes就直接对应元素数了。

基组库目录(dalton\basis)下的基组都可以用basis或atombasis来使用，基组名就是基组文件名字。赝势都在basis/ecp_data里，可以通过ECP=xxx来使用。比如可以Basis=stuttgart_rlc_ecp ECP=stuttgart_rlc_ecp，因为无论是这个基组名还是这个赝势名都在basis和basis/ecp_data里有同名文件。

由于Dalton的.mol文件格式定义得很麻烦，得一类一类定义，因此不好从结构文件或其它量化程序的输入/输出文件里直接粘过去，因此最好的做法就是用Multiwfn产生Dalton的输入文件。启动Multiwfn后，载入任意一个含有结构信息的Multiwfn支持的格式，比如wfn、fch、molden、pdb、xyz、mol等，然后依次输入
100 //主功能100
2 //导出文件
19 //导出Dalton的输入文件
idol.dal //导出的.dal的文件名。不需要产生它的话这一步直接按回车
master.mol //导出的.mol文件名
此时当前下就有了idol.dal和master.mol。这个.dal文件对应B3LYP单点计算。.mol文件包含此体系结构，并且对应使用6-31G*基组、不利用对称性的情况。之后大家根据实际计算要求对这两个文件进行修改即可，比手动从头写它们方便多了。

↧

2018年下半年观看的非TV版动画简评

January 1, 2019, 2:48 am

≫ Next: DFT-D4色散校正的简介与使用

≪ Previous: 量子化学程序Dalton的编译方法和运行方式简介

2018年下半年观看的非TV版动画简评

文/Sobereva 2019-Jan-1

在12月上旬去大阪采风期间，在Toho cinema电影院看了以下三部动画

↧

DFT-D4色散校正的简介与使用

February 13, 2019, 3:52 am

≫ Next: 2018年末在大阪入的二次元相关物品

≪ Previous: 2018年下半年观看的非TV版动画简评

DFT-D4色散校正的简介与使用

文/Sobereva@北京科音

First release: 2019-Feb-13 Last update: 2019-Feb-14

之前笔者在《DFT-D色散校正的使用》（http://sobereva.com/210）中详细介绍了DFT-D3的函数形式以及使用方法，还有其它相关的文章：《DFT-D色散校正的使用》（http://sobereva.com/210）、《谈谈“计算时是否需要加DFT-D3色散校正？”》（http://sobereva.com/413）。大家如果对DFT-D3尚不了解的话请先阅读以上几篇。本文笔者简要介绍一下DFT-D3的后继者DFT-D4以及其实际使用方法。由于笔者精力有限，此文在原理方面就不写得很详细了。

1 关于DFT-D4方法

DFT-D3色散校正如今已极度流行，不光可以使那些计算弱相互作用差的泛函在计算弱相互作用精度方面有质的改进，对于计算很多中、大体系，特别是涉及过渡金属反应的热力学数据往往也有明显改进。DFT-D3最大的一个软肋就是没法考虑体系的实际电子结构。同种元素的原子，在不同化学体系中的电子结构显然是不同的，这从原子电荷上就可以直接体现出来。特别是过渡金属，在不同配合物里往往以不同氧化态形式存在，虽然其原子电荷的差异没有形式上的氧化态的差异那么夸张（参见《使用Multiwfn通过LOBA方法计算氧化态》http://sobereva.com/362里的一些论述），但是差异还是相当显著的。DFT-D方法计算色散校正能是基于原子的色散系数计算的，这从《DFT-D色散校正的使用》一文的公式里可以看得很清楚。实际上原子的色散系数是显著依赖于原子的电子结构的，特别是原子电荷这个直接表征原子在分子中带的净电荷的量对色散系数的影响是明显不可忽视的。但是由于DFT-D3没有考虑这点，而只纯粹依赖于体系的几何结构，当体系中存在显著带电的原子的时候，比如过渡金属配合物、离子化合物，DFT-D3在原理上就不是特别理想了（尽管从实际表现上来看，对于牵扯过渡金属的体系，用DFT-D3比不用一般还是明显有改进的）。

色散校正的方法很多，有的是像DFT-D3一样不考虑实际电子结构，如OBS、DFT-ulg；也有的是能体现实际电子结构的，如XDM、dDSC、TS、LRD、vdW-DF/VV10、MBD@rsSCS等。那些能体现实际电子结构的做法普遍比形式超级简单的DFT-D3更昂贵，编程实现往往更费劲，大多没有解析梯度，被主流程序支持得也比较少，比如笔者撰文时最新的G16 B.01一个都不直接支持，而ORCA 4.1.1版只支持VV10（也被叫做DFT-NL）。

为了解决DFT-D3的上述不足，Grimme在JCP, 147, 034112 (2017)中提出了DFT-D4，关键性的改进就是让原子色散系数与原子电荷挂钩，从而能更好地反应实际情况。2017年这篇文章实际上是DFT-D4的最初版，发表之后，Grimme一直也没公开提供能做DFT-D4计算的程序，令人觉得很莫名其妙，不禁猜测是不是DFT-D4还存在什么问题。后来在2018年7月，Grimme往ChemRxiv上上传了介绍DFT-D4最终版文章的v1版，在2019年1月25日又上传了这篇文章的v2版，参见https://doi.org/10.26434/chemrxiv.7430216.v2。我估计过不多久，这篇介绍DFT-D4最终版本的重量级文章就会正式在期刊上发表了。目前计算DFT-D4的程序已经公开了。

根据这篇预印版的DFT-D4最终形式的文章，可以看到最终形式的DFT-D4会有以下特征：
·和DFT-D3(BJ)一样使用BJ阻尼函数。目前DFT-D4已经对所有主流泛函都拟合了阻尼参数
·带有和DFT-D3一样的Axilrod–Teller–Muto (ATM)形式的三体校正项。DFT-D4也可以结合MBD形式的三体校正项，但更为昂贵，而且实测的精度并没有ATM那么好
·色散系数依赖于electronegativity equilibration (EEQ)方法计算的原子电荷。EEQ这个方法和已经很流行的EEM方法差不多，都是基于电负性均衡原理的思想，依赖于和元素有关的经验参数，可以瞬间计算很大体系的原子电荷。EEM的一些介绍可以看Multiwfn程序手册的3.9.15节
·有解析梯度。这是VV10之类其它依赖于电子结构的色散校正方法所不具备的
·最高支持到86号元素（Rn）
·和DFT-D3一样基本上都是零耗时
·根据Grimme的测试，DFT-D4的精度能达到VV10这样更复杂的色散校正方法的精度，甚至有时更好

对于那些不存在显著带电原子的情况，D4和D3精度半斤八两，至少不输于D3。而对于有显著带电原子的情况，D4比D3的改进还是挺明显的，除了上述提到的Grimme的D4相关文章里有体现外，还可以看他的Acc. Chem. Res., 52, 258 (2019)，里面专门展示了DFT-D3、D4在金属有机体系上的效果。

DFT-D4原理上也可以结合其它原子电荷。2017年那篇JCP里初代DFT-D4结合的是GFN-xTB方法（一种半经验形式的DFT方法，类似DFTB）计算时顺带产生的Mulliken电荷，结合这种电荷时被称为DFT-D4(TB)，但测试发现这种形式不仅算原子电荷的过程更麻烦（需要依赖于专做GFN-xTB的xtb程序），增加了耗时，结果还不如结合EEQ电荷的最终版DFT-D4好。

Grimme的文章也表示，DFT-D这种色散校正形式到了DFT-D4这一代就基本没有油水进一步可榨了。由于最终形式的DFT-D4计算又快效果又好，应该在未来会很快普及、被大量量化程序直接支持。而且笔者也认为，有了DFT-D4，VV10等绝大部分以往提出的能够展现实际电子结构的色散校正方法就可以彻底退出历史舞台了（但有个别这些方法由于仗着更高级的计算形式，精度可能做到比DFT-D4更高一些，所以还不是完全没存在意义）。

当然，未来肯定有很多DFT-D4相关的测试文章接踵而至，也不排除DFT-D4方法的定义又出现一些改变，以上说法只是笔者撰文时的情况和看法。

2 Grimme的dftd4程序

2.1 简介

Grimme写的独立的做DFT-D4的程序dftd4已经发布在了https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/dftd4，可以直接下载源代码包。下文说的是笔者2019年2月13日在此处下载到的dftd4.2.0.tar.xz的情况，以后版本可能有些地方会有变动。

这个DFT-D4程序用法、用处和DFT-D3很相似。由于此程序里面没有包含xtb程序，因此做的DFT-D4只能是基于EEQ电荷的（如上所述，这也正是标准的DFT-D4的情况）。此程序的三体校正项支持前述的ATM和MBD形式，因此确切来说，此程序可以算的DFT-D4具体形式包括DFT-D4(EEQ)-ATM和DFT-D4(EEQ)-MBD。

dftd4得先编译才能运行。为便于读者使用，按照本节做法编译好的Linux版和Windows版我直接提供在此：http://sobereva.com/soft/dftd4.2.0_binary.rar。其中有.exe的是Win32版，没后缀的是Linux版，都是可执行文件，直接就能运行。

2.2 最简单粗暴的编译方法

下面说一下如何以最简单的方式编译。

Windows 32bit版：笔者机子里装了Visual Studio 2017以及Intel Parallel Studio XE 2019 Update 1里面的Intel Fortran compiler和Intel MKL库。启动Visual Studio 2017，新建一个项目，把dftd4压缩包里的include目录下的.f文件和source目录下的.f90文件都放到项目的文件夹里，并且加入项目里。把编译的配置从默认Debug改为Release。之后在项目属性里，在Fortran标签页下把Libaries里的Runtime Library设成Multithreaded，Use Intel Math Kernel Library设Sequential。Language标签页里Process OpenMP Directives设Generate Parallel Code。之后如果你愿意的话还可以去设对CPU和指令集的优化选项，这里就不用了。然后对项目直接编译，项目目录下的Release目录里就产生了dftd4.exe可执行文件，直接就能用了，而且传给别人别人也能用。

Linux版：笔者的机子里已经装了Intel Fortran compiler 19.0.1.144和MKL数学库（是按照《VASP最简单的安装方法》http://sobereva.com/455里面的做法装的Intel Parallel Studio XE 2019 Update 1里面的）。将dftd4压缩包解压后，将include目录下的.f文件拷入source目录，再进入source目录，直接运行以下命令即在当前目录下产生了dftd4可执行文件
ifort *.f90 -qopenmp -qopenmp-link=static -mkl -static-intel -stand f08 -check bounds -o dftd4
其中那些带static的选项是为了让编译出的可执行文件不依赖于动态库，从而在别人的机子里也确保能运行。

2.3 标准但麻烦的编译方法

dftd4基于meson+ninja的代码生成系统组合，如果你想形式上最“优雅”地编译（其实没任何好处），需要系统里有meson和ninja。这俩玩意儿比较新，可能很多人不熟悉，这俩程序其实就相当于常见的cmake和make，只不过有一些额外的特点而已。笔者认为DFT-D4这么简单的程序用mason+ninja纯粹是莫名其妙，也给用户添麻烦，一般系统里都不自带它们，还得现装。下面我们来通过meson+ninja编译DFT-D4，机子里已经装了上述Intel Fortran编译器和MKL库。笔者也尝试了用此系统自带的gfortran 4.8.5，发现编译不过去。

先运行以下命令以安装meson、lapack静态库（顺带会安装blas静态库）、ninja。由于yum这么安装之后ninja的可执行文件名是ninja-build，所以得做个符号链接成为ninja
yum install lapack-devel
yum install meson
yum install ninja-build
ln -s /usr/bin/ninja-build /usr/bin/ninja

将下载到的DFT-D4程序的压缩包解压，进入此目录，直接将以下内容输入命令行窗口，就会通过ifort来编译
FC=ifort meson setup build && ninja -C build
然后在当前目录下的build目录下就出现了名为dftd4的可执行程序，可以直接用了。编译过程中终端里会提示什么不识别-pipe之类选项的警告，不用管它，只要程序能用就行了。如果想运行得更快，而且你的机子里有MKL库的话，可以把编译时依赖的lapack给替换为MKL库，把dftd4目录下自带的meson.build替换为我提供的这个即可：http://sobereva.com/attach/464/meson.build。

2.4 基本用法

在含有dftd4的目录下直接用./dftd4就可以显示出此程序可以接的选项，一看就懂，就不多说了。比如下面的命令是对H2O.xyz这个文件里的体系基于BLYP泛函的参数计算标准形式的DFT-D4，即DFT-D4(EEQ)-ATM形式的色散校正能
./dftd4 H2O.xyz --func blyp

瞬间看到以下信息
           -------------------------------------------------
          |                Calculation Setup                |
           -------------------------------------------------
   coordinate file      : H2O.xyz
   number of atoms      :      3
   charge               :      0
   non-additivity corr. : ATM
   charge model         : EEQ
   functional           : b-lyp
   omp threads          :      1
   memory needed (est.) :    0.0 Mb

O      q(ref)        CN(ref)   cov. CN(ref)     α(AIM,ref)
     0.0000000      0.0000000      0.0000000      5.1967092
    -0.3547147      0.9924594      0.8041679      6.1223924
    -0.5988153      1.9886928      1.6112394      6.7491941
     0.0000000      0.9985672      0.9798440      5.1987934
H      q(ref)        CN(ref)   cov. CN(ref)     α(AIM,ref)
     0.0000000      0.0000000      0.0000000      5.0540161
     0.0000000      0.9117922      0.8942243      2.7207580

           -------------------------------------------------
          |               Damping Parameters                |
           -------------------------------------------------
   s6                   :     1.0000
   s8                   :     2.3408
   a1                   :     0.4449
   a2                   :     4.0933

           -------------------------------------------------
          |                     Results                     |
           -------------------------------------------------
Edisp /kcal,au:    -0.2980 -0.00047485

dispersion energy written to file .EDISP

即色散校正能为-0.00047485 Hartree。如果你用cat .EDISP显示刚产生的.EDISP隐藏文件，会看到更高精度的数据：-0.00047485257046358403。

dftd4另外常用的选项是--chrg，用于设定体系净电荷；--grad，用于计算色散校正能的梯度；--hess，用于计算色散校正能的Hessian。

3 在量子化学程序中使用DFT-D4

ORCA从4.1开始支持了DFT-D4，实际上是调用程序目录里otool_dftd4可执行文件算的，这个文件其实就是专供ORCA的dftd4。只要在ORCA输入文件里简简单单地写上D4关键词，计算时就会自动计算出D4校正能并加到总能量上。ORCA也支持DFT-D4下的优化任务。

对于笔者撰文时最新的ORCA 4.1.1，大家会发现ORCA输出的DFT-D4校正能和直接用Grimme的dftd4程序给出的不同（选的都是相同泛函的情况下）。这是因为起码对于ORCA 4.1.1来说，默认算的是DFT-D4(TB)形式的校正能，因此计算时会自动调用ORCA自带的otool_xtb（专供ORCA的xtb程序）做GFN-xTB计算。由于DFT-D4(EEQ)-ATM形式更便宜且结果更好，我预感ORCA以后早晚会把D4关键词的默认情况改成DFT-D4(EEQ)-ATM形式。

顺带一提，日落西山的Turbomole从7.3也支持了DFT-D4。

不知Gaussian什么时候会正式支持DFT-D4，估计是早晚的事。对于尚不支持DFT-D4的Gaussian，如果想在Gaussian计算中使用的话，可以利用《将Gaussian与ORCA联用搜索过渡态、产生IRC、做振动分析》（http://sobereva.com/422）和《将Gaussian与Grimme的xtb程序联用搜索过渡态、产生IRC、做振动分析》（http://sobereva.com/421）里介绍的Gaussian的external关键词自己写个接口让Gaussian可以在计算能量、受力、Hessian的时候调用DFT-D4，实现起来很简单。

↧

2018年末在大阪入的二次元相关物品

February 18, 2019, 6:58 am

≫ Next: 2018年末在大阪、京都采风时的与二次元相关的见闻

≪ Previous: DFT-D4色散校正的简介与使用

PS: 本文图非常多，90多张，24MB，请非常耐心等待加载...

2018年末在大阪入的二次元相关物品

文/Sobereva 2019-Feb-18

2018年12月去了趟大阪和附近地区，其中与二次元有关的记录见《2018年末在大阪、京都采风时的与二次元相关的见闻（http://sobereva.com/466）。此文把这次途中购入的二次元相关物展示一下。这是所有购入的物品汇总。下面挨个依次说说（PS：屋内光线不好，本文中很多照片颜色比实物暗淡得多，存在明显色差）

下面这些主要是在animate买的。

《少女歌剧》的ED和《终将成为你》的OP。我很喜欢少女歌剧TV版动画，不过其ED我倒觉得一般，不过这CD的封面实在太好，所以入了。《终将成为你》的OP极其出色，画面也超赞，这动画也是神作级别的，这CD有很强的收藏价值。

《终将成为你》漫画第一卷，以及此作的佐伯沙弥香的外传小说。

《终将成为你》不仅动画绝赞，原作质量也非常高。可见动画和漫画的画风、整体风格都很相似

之前就听说有佐伯沙弥香的外传，起初以为是漫画，买到之后才知道是小说。而且不是《终将成为你》原作者的小说，而是另外的写同人作品有名的人间人间写的，但里面的插画都是《终将成为你》的原作画的。沙弥香也真是有故事的人，原本和那个前辈在一起挺美好的，可惜那个前辈变心了。沙弥香小时候也和其他妹子有过美好的邂逅。沙弥香可谓从小就是生活在百合园的少女。

《我被最想拥抱的人威胁了》里面总是对西条高人发情的东谷准太的夹子。这个夹子设计得不错，夹子冲上，而且是安放在最下方，因此可以夹住东西立起来，实用性较高。

我超超超级喜欢的《高分少女》动画的原作漫画，没看过此动画的人强烈推荐一看，我吐血推荐，特别纯洁特别有爱。当时店里总共有1~7卷，我很想知道TV版动画之后的故事，但也不知道动画版播到漫画的哪里了，就买了5、6、7卷，发现第5卷基本上是和动画末尾接上的，也就是日高小春要求男主跟她对战，赢了他就得和自己交往那个剧情之后的内容。

每一卷第一页都有一些有意思的图。

此作漫画的水准高于我的预期，没想到漫画也这么好看。作者想象力非常丰富，古烈存在感极高。即便日语不擅长，连蒙带猜也基本能看明白漫画的意思。里面出现了修罗场，到最后果然如我预料的，终于日高小春和大野晶通过街霸展开了堵上男主的决战。虽然只是漫画，从形式上来说表现力注定跟动画没法比，但战斗过程精彩程度看得我依然沸腾了。其实我这次去animate的时候，貌似之前已经发售了第8卷，可惜没看到有卖的，真想知道到底是谁赢了（按理说大野晶不可能输，除非小春又玩儿赖）。我估计看过动画版的人，看了下面几页，已经被吊足了胃口了。

《牵牛花与加赖同学》动画的公式书，包括插画、访谈等。这是一部非常好的百合剧场版动画，这俩人特别有爱，ED动听至极。

这些插画真是棒极了！太般配了！

书中CV访谈。佐仓配加濑实在太合适了，CV本人和加濑有微妙的相似（对软萌妹的痴汉心态）

阿丝娜的行李箱贴纸，为了送一个阿丝娜控的女死宅买的

贴纸背面，以及阿丝娜的钥匙扣

夜羽的魔术贴。这个东西有两层，之间是魔术贴相连，下面那层可以缝到包上。

黛雅的胸章，神情很美

随机胸章，抽到的小曜是我很喜欢的，表情很爽朗

梨子的亚克力指扣和随机抽出来的小曜的徽章

梨子和夜羽的行李箱贴。这个我可不敢贴在容易蹭到的地方，要不然蹭花了太心疼，我都贴到了虽然不那么显眼但也不容易蹭到的地方。

黑子的徽章，黑子贫瘠的身材实在太性感了

夜羽的方巾。我可舍不得用

黛雅的眼镜布。我直接在家挂起来了，也舍不得用。黛雅虽然乍一看好像是冰冷美人，但实际上性格也很跳脱，活泼起来的时候一点也不输于其它人，这图显得很有元气

lovelive手游水团的卡牌的公式书。这个超值，非常厚，里面整体作画质量很高，有不少画面可谓极品。看此书时可以把此书收录的时间段内的所有水团卡牌尽收眼底，对于玩ll手游的人颇具价值。而且会发现，原来很多卡的图像是一张完整的大图拆分开的，看了此公式书终于才一次性看到了全貌。

书里内附的拉页。

之前真没想到居然这两张卡其实是在一起的，感觉鞠莉X夜羽的CP也可以有，鞠莉可以把夜羽弄得很开心，俩人都超有个性。

书末的目录

《猪头》里的双叶理央和《偶像大师灰姑娘女孩》里的双叶杏的亚克力立牌。杏子好可爱。还真是超巧，写本文的时候突然发现俩双叶正好在这里碰上了。

《点兔》期间限定展购入的理世的亚克力立牌和鸭居燕的立牌。理世是《点兔》里我最喜欢的角色，很帅气。鸭居燕这个角色真是特别好，看《我家女仆有够烦》最后两话之前我喜欢她主要是感觉她的方方面面都特别有意思，但看完最后两话之后，我同时也感觉她也是一个值得尊敬的人。

梨子的手持拍摄牌。之前在《2018.4在大阪所购的二次元物品》（http://sobereva.com/416）里买过夜羽、黛雅和小曜的这种拍摄牌。梨子的腿真是超美啊！细长粉嫩。旁边的是Rider的立牌，行头太性感了，令人忍不住入手

《高分少女》里我酷爱的绝对无口的大野晶的挂饰和夜羽的圆珠笔。这个挂饰还挺有想法，把沉默不言的对话框分离提供

《魔法少女小樱》里小樱的挂饰，是个金属的薄片，金闪闪很漂亮

水团的贴纸，可以贴日历上，但是我舍不得用。有些表情挺萌的

文件夹。这个像淋湿的乌鸦一样的夜羽的神情，仿佛向我诉说着恶魔的低语。梨子是形象很矜持的少女，但是在这个文件夹里却意外地展露出了色气，令我忍不住买了

背面，每个角色都有一个突出角色特点的特征性的图标，设计得相当好

现在ll新企划虹咲学园的周边也已经上了，近江彼方是其中我最喜欢的之一，迷迷糊糊很萌，有点像双叶杏。之前我抽到过果南的这张SSR，被她的豪放的欧派给震撼了，这张图给我留下了深刻印象，没想到居然还能碰到对应的文件夹，果断入。

没想到现在animate还有很多东方物在售，很高兴地看到有我酷爱的蓝大人的挂扣和胸章，果断入

黑白的挂饰。我对黑白本身兴趣一般，不过这个挂饰做得真是挺精美的

我对咲夜不算特别感兴趣，不过这个文件夹上的咲夜真是几乎所有我看过的咲夜的图里最可爱的，令人心动啊，画得太赞，神情温柔可爱，气氛感也特别好，令人忍不住想拥有

文件夹三件套。我看到夜羽的这个拳击手的图案的时候，瞬间就被萌杀了！夜羽怎么能这么可爱！这新发型太有冲击力了。可惜没法单买夜羽的，只能连同花丸和露比的一起买。

买了个爱酱的小粘土。表情随机，抽到的这个还不错

由于洒家在animate开销大，店员送了偶像大师的明信片和书签

这是animate的新品目录和预告

没想到在大阪机场的玩具店里看到有卖爱酱的粘土。其实我对虚拟偶像爱酱本身没有多大兴趣，但这个粘土的表情做得实在太可爱了。我犹豫了好久，终于还是买下了。我感觉碰见喜欢的东西，只要价格不离谱，就应该出手，否则以后想买都没机会了。

这个粘土的可玩性极高，所有关节都能动，而且配件丰富，我真佩服奸笑社。而且还给了个框，可以摆成正在直播的样子。

这是机场的宠物小精灵专卖店购的收纳药品之类的小包

皮卡丘的筷子

下面这些是lashibang买的。

虽然我不玩桌游，但是看到自己喜欢的角色的漂亮而且便宜的牌还是忍不住买，在lashibang里看到好几排玻璃柜展示出售的卡牌。我买的夜羽和希的卡真是漂亮啊~。另外两个怪兽娘的卡牌是《2018年下半年观看的非TV版动画简评》（http://sobereva.com/456）里提到的看《怪兽娘黑》给的观影赠品抽到的，没抽到我大爱的black的卡真是遗憾，不过其中抽到一个“正义”一方的巨乳白色战斗服的那个倒也还行。

这是在lashibang中古店买到的绫波的手办。我在那家店反复精挑细选了很久，那里有不少绫波的手办，但就这个是表情最自然，能传递出绫波女神的神韵，而且展现出了纤细修长的漂亮身材。而且难得的是价格还很便宜，性价比超高，真是没白费劲，找到宝了。其实有时候我觉得费半天劲去淘，关键倒也不是为了少花钱，而是为了能享受能买到性价比极高的物品的喜悦。

这是lashibang搜罗到的K-ON的小粘土，很可爱，作为这样质量的全新品这价钱太值了，也正是我想要的（呆唯那个除外）

分解图。三个角色间可以相互换脸换身体换发型

把所有这次买的手办和亚克力立牌合在一起照一张

夜羽的挂饰和梨子的胸章。这都是二手物，只有在lashibang这样的店里才能搜罗到。尤其是胸章做得特漂亮，在阳光下金闪闪，相机拍不出效果来

小焰的金属指扣，金色光泽很漂亮

京都漫画博物馆买到的我首席妻子MIO的T恤。能买到这个实在太难得了，真是宝物。K-ON的东西在卖新货的animate是买不到的，真没想到竟然漫画博物馆有全新的卖，难道和离京阿尼公司近有关系？MIO的这个图案实在太美了，全面展现出最具有MIO特征的美，黑亮亮的眼眸太漂亮了。我的ACG T恤已经很多了，这是目前我最珍贵的一件了。（价钱虽然不便宜，300多，但值得）

京都漫画博物馆买的鲁路修的钥匙扣。鲁路修是我最钦佩的男性角色之一

下面是其它的在《点兔》的期间限定展览购入的

点兔的文件夹套装

理世的马克杯，这也是现在我喝可可之类常用的杯子

千夜的磁贴。虽然我对千夜算不上特感兴趣，但她的这个姿势实在很帅气，把我帅到了

十抽一抽出的胸章。虽然这个图案也挺可爱，可惜是个我根本记不住名字的角色。

限定展送的智乃的明信片、随机抽的maya的指扣、千夜的徽章。手气真是不行，我喜欢的rize、纱路、智乃都抽不出来。虽然我对maya一点兴趣也没有，但考虑到她的CV是德井青空，感觉抽到的这个还有那么一点价值。

点兔的塑料海报，我在家里已经挂起来了

这不是买的，是在Toho Cinema看《哥斯拉（GODZILLA）噬星者》剧场版动画的时候给的赠品。此作观感我在《2018年下半年观看的非TV版动画简评》（http://sobereva.com/456）里写到了。这个赠品还挺有创意，弄成了人类一方的机密文件形式。

这是在Toho Cinema看《ANEMONE/交响诗篇艾蕾卡7 Hi-evolution》动画的赠品色纸。

↧

2018年末在大阪、京都采风时的与二次元相关的见闻

February 18, 2019, 7:35 am

≫ Next: 简化用了IOp(9/40=x)的Gaussian的CIS/TDDFT任务的输出文件的程序：simpIOp940

≪ Previous: 2018年末在大阪入的二次元相关物品

PS：本文图很多，110多张，34MB，请非常耐心地等待加载！

2018年末在大阪、京都采风时的与二次元相关的见闻

文/Sobereva 2019-Feb-18

2018年年末去大阪及附近呆了10来天，购入的与二次元相关物在《2018年末在大阪入的二次元相关物品》（http://sobereva.com/465）里进行了完整展示。此文里我把在这期间看到的与二次元有关的事物简单聊聊。途中照片总共照了800张左右，不可能在这里都发出来，本身也不是游记，所以只把和二次元有直接关系的图发一下。

1 《请问要来点兔子吗》主题展览

在大阪的一家百货商店的一层橱窗里，意外地看到居然有庆祝智乃生日的event。点兔里全是可爱萌妹，这谁顶得住啊！

里面是展览+周边销售。琳琅满目。我去得有点晚，不少东西都已经完售了，还不然我还能多买点我最喜欢的理世的周边。我购买的时候已经极大地克制住自己的消费欲望了，要不然还得多花50%的钱。我看到有的男性上班族挺疯狂的，买那种角色随机的小周边，一买就买一大把。那个RABBIT HOUSE的茶挺有创意的，有点想买。

这个给智乃庆生，能自己写留言的地方设计得真是太好了，特别有爱。智乃好可爱！这大抵是我第一次觉得智乃这么可爱，当初看动画的时候都没这么觉得。看过这次展览之后我对《点兔》的喜欢程度大大加深了。

在同一层还有其它的女性向作品的展览，我不认识，里面的角色全是男青年，就没怎么仔细看。在旁边有个高清电子屏幕，里面Show by Rock!!里的希安可以做出各种动作和表情，感觉挺有意思的。

2 大阪环球影城

大阪环球影城名气很大，看名字我本以为是个大型的放映电影的地方，去了才知道其实是个电影和动画的主题游乐园。去的时候临近圣诞节，环球影城完全布置成了圣诞风格。总的来说，环球影城不错，玩的东西挺多，但最大的缺点就是人太多（令我回想起当年参加上海世博会的情况），比较热门的游乐设施得排一两个小时，我去的时候还不算特别旺季都这样。之前我在九州旅行的时候去过豪斯登堡，感觉环球影城和豪斯登堡很有类似之处，但我感觉相对而言还是豪斯登堡更爽一些，印象中规模更大一点，而且游客也就环球影城的几分之一吧，很少需要排队，我强烈推荐一去。那时候在豪斯登堡看到的灯光展是我活到现在看到的最壮观、宏大、璀璨的，令我心里大呼良心。不过环球影城的晚上的花车表演也很棒，很闪耀。

环球影城里小黄人主题的东西很多，不过我对小黄人毫无兴趣。不知道是不是这阵子正好赶上日本的中小学普遍组织休学旅行，在这里看到了大批女中学生，能看见很多漂亮细腿。确实如动画里常见的，尽管是寒冷的冬天，但大部分校服都是露腿的，而且绝大部分都不是穿肉色保暖袜来欺诈。

之前就听说森森森代言了某个药物的广告。去环球影城的途中居然真的看到了森森森的广告牌，感到挺意外。她这身打扮还不错。

有个场馆看完演出后购物区里的神奇女侠的画还挺帅的。

蜘蛛侠这个很好玩，进去之后坐在一个小车上，一会儿旋转一会儿突然加速，墙上投影的都是蜘蛛侠相关的战斗场面，还有各种体感效果，超级刺激。虽然排的人多，但也是绝对不可错过的。

环球影城里有个EVA主题的游乐设施。早上去的时候看到要排队时间太长，就想等着天黑了再去，没准人少点。结果天黑了，进场时候还是看到人的海洋。这个EVA的项目和蜘蛛侠那个有点像，同样是坐在可以旋转和加速的小车上，不过这个是带着VR眼镜的。这个项目非常好玩，自己会成为EVA和使徒在都市里战斗场面里的逃命的小老百姓，东躲西蹿，惊险得不得了，真没白排那么长时间的队。

到了晚上，一号机的头投影到墙上，感觉很有压迫感。

3 Toho Cinema电影院

在Toho Cinema电影院里看了三场剧场版动画：《ANEMONE/交响诗篇艾蕾卡7 Hi-evolution》、《怪兽娘黑》和《哥斯拉（GODZILLA）噬星者》，观感我在《2018年下半年观看的非TV版动画简评》（http://sobereva.com/456）里都评论了。

我实在颇喜欢《怪兽娘黑》，在大阪的商店街里就看到有这个动画的招牌，里面black的黑色皮衣包裹的白皙、傲人的欧派实在太吸引眼球、太诱人了。可惜电影院里没有这个动画的宣传海报，只能在门口的牌子照一张纪念。

电影院正好要放新出的龙珠剧场版，展示柜里有个龙珠实物，挺有意思

这次旅行非常遗憾的是，明明看到电影院有Bang Dream!的live现场直播，但是没买到票，如下所见已经完售了，真可惜。

4 京都漫画博物馆

在距离大阪不太远的精度有个漫画博物馆，不过这个和京阿尼没有直接关系。这个漫画博物馆貌似是基于一个历史悠久的小学扩建出来的。怕万一引起误会就没在里面拍照。这里面的日本漫画的藏书量或许是全日本最大的，真是漫画的天堂，包罗万象，就连上世纪初，在二战之前的日本漫画（那时候算连环画）都有。里面还有周边购物区、特殊活动室、特殊企划展。里面还有个厅专门放置知名漫画家给这个博物馆做的手模，就连因《向阳素描》而知名的苍树梅的手模都有，她的手比大部分其它漫画家的手都小巧（本身也是因为男性的手模居多）。

我去的时候正赶上纸芝居的表演，也就是那种洋片。在屋子里我和其它游客坐在椅子上，前面是个女性工作人员一边拉洋片一边跟观众balabala互动个没完，感觉下面来自各个国家的成年游客们像回到了幼儿园成为了小朋友似的，大家其乐融融，挺有趣，答对了问题还能从她那里拿到小奖励。这个拉洋片的工作人员真是能说会道，即便来自西方的语言和她不通的大叔也能被她带动起来。感觉干这种工作真得是那种特别热情、特别外向的人才行。

导游小册子

5 京阿尼公司

造访京阿尼公司这个特别值得好好一说。业界里，我最佩服的就是京阿尼，从当年的《轻音少女》到近年来的《紫罗兰》，都是我心目中的极致，不管哪部作品都制作极其用心（虽然并不是每部动画都很合我的胃口）。在无数次观赏京阿尼的作品时我都佩服得五体投地，赞不绝口。由于京都离大阪不远，我就亲自造访了京阿尼总部。

那天是先去漫画博物馆然后再去京阿尼那里的，没想到京阿尼居然那么早就关门了！吃了闭门羹，但直接回去又太舍不得，就在附近反复转悠。下面就说说京阿尼公司的外围环境吧。

去京阿尼通过城铁比较方便。这是京阿尼那一站

这就是传说中的京阿尼总部了！无数极其优秀的作品，就是在这貌不惊人的小楼里产生的！要是住在这附近多幸福啊，天天能看见京阿姨。

京阿尼公司比较偏僻，附近全都是矮小的居民楼，没有什么商业味道，很僻静，远离都市的喧嚣。感觉京阿尼就像一个隐士，悄无声息地在这个非常不起眼的乡间默默努力着。京阿尼的小楼地处非常狭窄的街道边上，是上坡区段。

上图向左看去，是下图的画面。京阿尼附近有一些中小学校，图中可见路过的学生妹。京阿尼作品中大量的中学生和校舍，或多或少从附近的学校那里有所取材吧。

京阿尼的小楼紧挨着道口。从小楼往右看去就是下图的景象。

之前看《踏切时间》的时候对道口产生了浓厚兴趣，在《终将成为你》里面也把道口的魅力描绘到极致。看似平凡的道口其实是个很能蕴育故事的地方。试了一下，确实列车经过的时候哪怕在对方旁边说话，对方也听不见。

在大门紧闭的京阿尼公司门口仔细看了又看。京阿尼的小楼的一楼是个shop，可见现在主要卖的是《弦音》和《吹响!上低音号》的算是外传作品《利兹与青鸟》的周边。

进不去京阿尼的楼，直接走太可惜，于是就像痴汉一样绕着京阿姨的楼在附近绕了一大圈，看看附近的景色。京阿尼的楼背面是个幼儿园

再往后头走几步，是个漂亮的人行道，旁边是住宅

拐个弯，看到一个神社，里面还真有人认真地参拜。这令我不禁想起《弦音》里面泷川雅贵所在的那个寺庙，我想京阿尼的人应该肯定在这里取材过，毕竟离得那么近。而且我也感觉《弦音》里的居民楼和京阿尼附近的居民楼的风格挺像的。

再拐个弯，看到一些民居，这个枫树很漂亮

门前挂的这一串东西挺有韵味

11区在一些细节地方做得很好。井盖上都印着本地独特的logo

临离开京阿尼这片地区时天色已晚，没想到京阿尼的小楼竟然亮起了灯，还挺漂亮

在车站看到久美子、丽奈、希美、霙，感到特别亲切。我的丽奈太美啦！京阿尼GJ，我觉得京阿尼就是这一站的代表，像这样把京阿尼的作品放在旅客到达这一站时看到的最醒目的位置，想法非常好。来访者一看这个就知道没坐错站。

6 Animate和Lashibang

去了趟大阪的ACG比较集中的日本桥。不过当天时间过于仓促，只是呆了一下午，完全没过瘾。据说近期此处出现了坑爹女仆店，让女仆在街上招揽看着像光棍儿的死宅，拉到店里使劲宰，确实在街上看到有的女仆略可疑。

虽然哪家店都很有吸引力，但是时间紧，只能去最知名的animate，还有上次去熊本的时候逛得很开心的中古店lashibang。

lashibang的由于东西太多，手办和周边是作为两个店分开的。有点后悔在手办那个店和animate花的时间太多，导致如同藏宝库的卖周边的那个lashibang店只逛了20分钟左右，只探索了冰山一角。在手办店里精挑细选，反复斟酌，除购入的之外虽然还有其它好多很喜欢的，但由于行李箱有限，我又不是喜欢乱花钱的主，只能拍照纪念一下了。

刀剑神域外传的莲的这个手办做的不错

螃蟹公的这个手办我特喜欢，脂肪堆特别浑圆

索尼子cos成赫斯提亚，这俩人的乳量很相称

小暗的护士服

如果你亲自拿到这个，保证肯定忍不住各个角度仔细欣赏一番

应该是《挥动球与剑的少女》里的角色，衣不蔽体

没想到在lashibang还看到了当年我特别喜欢的《Rio Rainbow Gate》里理欧罗伦斯的手办，由于那个角色不算知名，能看到其手办感觉特别难得。但由于做得一般，就不展示了。

以下是Animate。大阪这家animate相当大，真是二次元天国，应有尽有。尤其是到lovelive的区，完全走不动道，感觉就像一般人看到一大片闪闪发光的金子。

店员做的《少女歌剧》的展台挺用心的

我挺喜欢这类等身大小的立牌，可惜没卖的，就算有卖的也没法完好运回家。我挺喜欢《月影特工》的

看到百合神作《终将成为你》的区我是很开心的，立刻入手

这次我深感ll、偶像大师、Bang dream!是当今三大支柱性少女偶像题材作品，在animate里都有专区售卖极其丰富的周边。我目前是ll深度入坑，偶像大师和Bang分别是中、浅度入坑。虽然偶像大师和Bang都营销得很棒，对我诱惑也不小，但我可不敢深入，因为我这次在animate深感，如果三个坑都入，在animate里我就得破产了！这次我主要是买ll买得很high，但还是极力通过理性克制自己的消费欲望，在某些物品买不买上纠结得要死。我很懂“阿宅的钱真好赚”的理，但明知如此，还是顶不住闪耀的二次元美少女们的魅力，花钱花得心甘情愿。

有一块区域专门卖cos衣服的。

桐人这个衣服有点想买，但由于嫌不好试穿，而且也差不多1200多RMB，偏贵，还是作罢了。

Fate也是大热门作品，店里有一大块卖Fate的区域

虽然东方的年代较早，周边也还是挺多的

离开日本桥区域的时候看到一个自动贩售机，居然有卖麻衣学姐代言的饮料！这必定得买啊！遗憾的是，凑过去一看，如下图可见，只有她代言的这款印着“桃”的饮料完售，而其它都有卖。果然二次元代言的效果太好了。可惜，这个贩售机在我经过的所有地方只有这一台，而且其它贩售机也都没有卖学姐代言的这款饮料，实在太遗憾了！我要是厂家的老板，绝对让所有食品、饮料都让二次元妹子代言。

之前听说过ll和樱花大战搞联动，图中还真看见了，花丸这身衣服还挺搭的

还看到的ll的街机，但是得回去了，没时间玩

7 机场

在大阪的机场，想不到能看到几家卖二次元相关物的店。这个Pokemon的店装饰得不错，在这里买了双筷子和药丸收纳袋

↧

简化用了IOp(9/40=x)的Gaussian的CIS/TDDFT任务的输出文件的程序：simpIOp940

February 19, 2019, 3:47 am

≫ Next: 谈谈势能面交叉对激发态优化的影响

≪ Previous: 2018年末在大阪、京都采风时的与二次元相关的见闻

简化用了IOp(9/40=x)的Gaussian的CIS/TDDFT任务的输出文件的程序：simpIOp940

文/Sobereva@北京科音 2019-Feb-19

简介

《Multiwfn支持的电子激发分析方法一览》（http://sobereva.com/437）一文全面介绍了Multiwfn支持的丰富的电子激发分析，其中有些功能是依赖于组态系数的。由于Gaussian默认情况下只输出绝对值大于0.1的组态系数，光靠这些对激发态描述的精度不够，因此对于Gaussian用户，用Multiwfn做那些电子激发分析时一般需要用诸如IOp(9/40=x)关键词来输出所有绝对值大于10^-x的组态系数（一般x=4）。但是此时造成的问题就是输出文件里的组态系数特别多，有人觉得通过这样的文件人工查看激发态主要信息不方便。

为解决这个问题，笔者写了个小程序simpIOp940，可在此下载：http://sobereva.com/soft/simpIOp940.rar

此程序可以载入用了IOp(9/40=x)的Gaussian输出文件，然后自行输入一个组态系数绝对值的阈值，程序就会把激发态的信息连同大于阈值的组态系数都输出出来，使得人工查看比较方便。

此程序文件包里带.exe后缀的是Windows版可执行文件，不带后缀的是Linux版可执行文件，Fortran源文件也附上了。

例子

例如此程序的压缩包里有一个uracil.gjf，TDDFT计算时用了IOp(9/40=4)，算出来的文件时uracil.out，里面列出的组态系数特别多：
Excited State   1:      Singlet-A"     4.7968 eV 258.47 nm f=0.0001 <S**2>=0.000
       9 -> 30        -0.00071
       9 -> 31        -0.00043
       9 -> 35         0.00028
       9 -> 67        -0.00011
       9 -> 73        -0.00016
       9 -> 76         0.00012
       9 -> 78        -0.00015
       9 -> 79        -0.00020
       9 -> 81        -0.00011
       9 -> 82         0.00023
       9 -> 88        -0.00021
       9 -> 89        -0.00059
...略

启动simpIOp940之后，输入uracil.out的路径，然后输入阈值0.1，当前目录下会产生new.out，这是处理好的结果文件，内容如下

Excited State   1:      Singlet-A"     4.7968 eV 258.47 nm f=0.0001 <S**2>=0.000
       26 -> 30         0.11588
       28 -> 30         0.67734
       28 -> 31         0.13625

Excited State   2:      Singlet-A'     5.4219 eV 228.67 nm f=0.1317 <S**2>=0.000
       27 -> 30        -0.13650
       27 -> 31        -0.14060
       29 -> 30         0.67086

Excited State   3:      Singlet-A"     6.0180 eV 206.02 nm f=0.0000 <S**2>=0.000
       26 -> 30         0.54135
       26 -> 31        -0.20634
       28 -> 30        -0.15424
       28 -> 31         0.36715

由于电子激发任务类型很多，此程序不一定兼容所有情况，碰见不兼容时请自行修改程序。

↧

谈谈势能面交叉对激发态优化的影响

March 2, 2019, 7:22 am

≫ Next: 考察SAPT能量分解的能量项随分子二聚体间距变化的简单方法

≪ Previous: 简化用了IOp(9/40=x)的Gaussian的CIS/TDDFT任务的输出文件的程序：simpIOp940

谈谈势能面交叉对激发态优化的影响

文/Sobereva@北京科音 2019-Mar-2

0 前言

TDDFT是目前最常用的激发态计算方法，以前在计算化学公社论坛上有很多次有人问为什么用Gaussian结合TDDFT优化的时候激发态顺序变化了、优化出来的激发态不是自己一开始要求的那个激发态之类的问题，这其实都是由于激发态势能面交叉所致，在本文就专门说一下这个问题。笔者假定读者已经阅读过这些文章了解了相关基础知识：《图解电子激发的分类》（http://sobereva.com/284）、《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》（http://sobereva.com/314）。看一下《使用sobMECP程序结合Gaussian程序搜索极小能量交叉点》（http://sobereva.com/286）对理解本文提到的一些概念也有帮助。本文用的Gaussian是G16 A.03版，轨道图形绘制和NTO分析都是Multiwfn 3.6(dev)做的。

1 透热态与绝热态

在讨论激发态优化之前，首先要弄清楚透热态和绝热态的概念，看下图

图中的态都是激发态，为了便于讨论假定都是单重态。FC结构指的是基态极小点结构。图中绿线和蓝线分别对应两个透热态势能面，可以认为每个透热态对应一种特定的电子激发模式，比如可以假设透热态1对应n->pi*激发，透热态2对应pi->pi*激发。当两个透热态能量相近时，由于态与态之间在一般会存在耦合（体现在相应的哈密顿矩阵非对角元不为0），两个透热态的波函数会混合产生出两个绝热态，对应不同绝热态势能面，在原本两个透热态相交的位置存在能量分裂。至于图上的棕色曲线，由于在图中的几何结构下与其它激发态势能面较远，因此既是透热态也是绝热态。

对于激发态优化过程中经历透热态交叉区域的情况，常用的S1、S2...这种称呼就具有含糊性了，必须得说清楚。如果你说的是透热态，那么按照能量由低到高编号的时候，得说清楚是对于什么结构而言的。比如上图中，在交叉点左边区域的S1（绿色曲线）到了交叉点右边就是第二激发态了，如果重新按照激发能排序，它就应该被称为S2了。而如果你讨论的是绝热态，按照绝热态能量由低到高来称呼S1、S2...，那就没有这个问题，比如图中的粉色虚线在各个位置下都是能量第二高的激发态。

2 牵扯势能面交叉时的激发态的几何优化

做激发态优化时，每一步都会算出一批激发态，那么怎么确定应当按照哪个激发态来优化？换句话说，应当在当前结构下对哪个激发态计算受力/Hessian来获得下一步的结构？不同程序有不同做法。Gaussian等一些程序的做法是根据组态系数，比较当前步算出来的各个激发态与上一步算出来的激发态的对应关系。比如上一步的时候感兴趣的态是能量第三低的态(i态)，因此上一步的时候受力/Hessian也是对这个态来算的，而在当前结构下，若发现能量第二低的态(j态)的波函数与上一步的i态最接近，那么上一步的i态就与这一步的j态产生了映射(map)关系，因此当前这一步感兴趣的态就是j态，计算接下来的位移所需的受力/Hessian也是对j态来算的。通过这种方法，Gaussian实现了所谓的state-tracking（态的跟踪）。

上面这种做法对于被优化的态不牵扯势能面交叉的情况完全稳妥（比如上图中棕线所示的第三激发态），但是当牵扯势能面交叉时，就有一些复杂情况了，见下图

上图体现从FC结构出发，优化FC结构下的第一激发态的过程。在当前结构逐渐移动到透热态交叉点附近时，接下来既可能沿着绿色箭头的方向走，从而最终优化到一开始所处的透热态势能面极小点上；也可能按照红色箭头走，最终优化到第一绝热态势能面的极小点上。根据Gaussian的state-tracking思想，由于沿着透热态优化每一步波函数特征改变较小，因此一般是沿着透热态势能面优化的。但是，也有时候，由于判断算法的不可靠或者一些数值因素，最终也可能会被优化到第一绝热态极小点去。究竟会出现哪种情况，有很大的运气因素，比如把步长上限改一下，或者用不同基组/泛函，最终就可能会被优化到不同的极小点去。因此得理清思路，搞明白到底出现了什么情况。

我们知道，在Gaussian的TDDFT计算时，我们可以通过root=i指定优化第i激发态。更确切来说，被优化的是在初始结构下按照能量排序的第i透热态（当然，由于Gaussian的state-tracking算法的不足，因此实际优化的结果并不一定是如我们所愿的那样）。由于可能优化过程中经历势能面交叉区域，因此通过root=i关键词试图优化第i激发态的时候，显然不能让总共被算出来的激发态数（nstates）也恰好等于i，否则可能当这个态与更高激发态出现交叉时导致跟踪透热态失败。笔者建议nstates设i+2或稍微更多一些。而且，就算是为了保证算出来的激发态本身比较准确，nstates也不应该正好顶着感兴趣的态来设，这在《Gaussian中用TDDFT计算激发态和吸收、荧光、磷光光谱的方法》一文中已经提过了。

对于很多体系，激发态，尤其是高阶的激发态能级分布特别密集，即有大量激发态势能面彼此十分接近。这个时候，你若想要求Gaussian优化你一开始用root关键词选定的态并一直在其透热势能面上行进，那真正达到目的几率可能较低，因为如前所述，很可能中途因为走上了绝热态的路径（某种意义上，类似于发生了内转换），结果最终跑到不是你真正感兴趣的透热态极小点上。

还有一种情况，是一开始用root指定优化不同的激发态，发现最终优化出的结果都一样，也是因为势能面交叉，并且Gaussian的state-tracking算法有所不足导致没法保证跟踪透热态所致，如下图示例的，可能一开始用root=1和root=2做优化，最后发现都优化到了第一绝热态极小点了。

3 SDNTO算法

2019年初在JCC上出了一篇文章（DOI: 10.1002/jcc.25800），提出了一种新方法来实现state-tracking，是基于当前步与上一步产生的NTO来比较当前步算出的各个态与上一步的时候被跟踪的态的重叠程度，重叠程度最大者就是这一步应当被跟踪的态。如果你不懂NTO，参看《使用Multiwfn做自然跃迁轨道(NTO)分析》（http://sobereva.com/377）。重叠程度计算方式如下

其中n是当前步，n-1是上一步，φ是NTO轨道波函数，c是NTO的本征值，只有大于人为设定的阈值的NTO才纳入上述加和。文中基于这种思想，结合很简单的最陡下降法，提出了所谓的Steepest Descent minimization using Natural Transition Orbitals (SDNTO)方法来试图确保在优化中能够跟踪透热态。实测发现，即便对于激发态能级很密集的配合物，这种算法也能成功跟踪一开始指定的透热态。下图是SDNTO文章中通过SDNTO算法优化cis-(Cl,Cl)[RuCl2(NO)(tpy)]+配合物的第9透热态的过程，横坐标是优化的步数，图中不同颜色表示每一步结构下的不同的绝热态激发能。可见对于这样势能面交叉复杂的情况，SDNTO方法也很好地跟踪了指定的透热态，而原文说Gaussian自己的算法对此体系是失败的。

SDNTO这种算法目前没有公开的程序实现，作者自己的程序也是通过外挂Gaussian实现的，究竟SDNTO算法是否普适、效果好坏是否严重依赖于人为设定的参数，那还是未知数。顺带一提，如果你想计算两个结构中的各个轨道间的重叠积分的话，用Multiwfn就可以轻易实现，有专门的功能，看Multiwfn手册3.200.6节的例子。Multiwfn可以在http://sobereva.com/multiwfn免费下载。由于Multiwfn有这个功能，再加上Multiwfn可以直接产生记录了NTO轨道的fch文件，其实借助Multiwfn自己写一个基于Gaussian实现SDNTO优化的程序也并不复杂。不排除可能在以后的Gaussian中会直接支持SDNTO方法。

4 涉及激发态势能面交叉的Gaussian TDDFT优化一例：胞嘧啶

胞嘧啶(cytosine)这个体系在SDNTO文章中做了研究，文中提到在距离FC结构很近的地方就有S1和S2间的圆锥交叉。这里我们用Gaussian实际做一下TDDFT对S1和S2的优化，看看是什么情况（笔者算出来的结果和SDNTO文章所述的有所出入，下文根据实际算出来的情况说事）。计算涉及的输入输出文件都可以在这里下载：http://sobereva.com/attach/468/file.rar。初始结构是PBE0/6-31G*优化的基态结构，为稳妥起见激发态计算都是设nstates=5。为了与SDNTO文章一致，激发态计算用的是PBE0/6-31+G*。

Gaussian的TDDFT优化的每一步都会输出当前结构下所有激发态信息，输出文件里会看到“Excited State 1:"、“Excited State 2:"等等。此处Excited State x相当于在当前结构下，被Gaussian判断为与初始结构下第x态相映射的态（即对应同一个透热态）。当然，Gaussian判断得是否合理那不一定。

4.1 默认步长下优化S1

我们先来优化S1，这里用默认步长，输入文件是文件包里的S1_defstep.gjf。当前我们设的是root=1，因此，每一步中被Gaussian标记成"Excited State 1"的态就是被优化的态，每一步的受力/Hessian都是对当前被标记成"Excited State 1"态来计算的。

把.out文件中所有含有"Excited State 1"和"Excited State 2"的行里面的激发能提取出来，绘制成激发能随优化步数的变化，得到的图如下所示。为了把细节看得清楚，图中只展现了前12步

由图可见，在第3步的时候两个激发态能量几乎相同，明显出现了交叉。当前优化过程在经过交叉点时并没有理应地在透热态势能面上进行，而是最终走了绝热态的势能面，也即对应"Excited State 1"的黑色曲线在交叉点右侧都是能量最低的，这可以算是体现了Gaussian的state-tracking算法的失败。

由于当前没有一直在最开始的S1透热态上走，而是中途切换到了S2的透热态去，因此，优化第一步的"Excited State 1"的电子激发特征和最终结构的"Excited State 1"的电子激发特征必然不相符。为了更好地说明这一点，我们下面通过轨道考察一下电子激发特征。

FC结构下S0->S1的跃迁几乎完全对应HOMO->LUMO跃迁，两个轨道图形如下，可见是pi->pi*跃迁。

FC结构下S0->S2的跃迁缺乏主导的MO跃迁，因此使用Multiwfn转化为NTO跃迁的方式描述，可几乎完美地表示为NTO29->NTO30，由下图可见是n->pi*跃迁，而且孤对电子同时明显来自N和O。

下图是在我们刚才做S1优化得到的结构下"Excited State 1"的跃迁方式，可以用NTO29->NTO30完美描述，可见明显是n->pi*跃迁。

一对照就看出，我们所优化的出态，也就是被Gaussian标记为"Excited State 1"的态，其实对应的是FC结构下的S2透热态，优化过程并没有从始至终一直在S1透热态上走。

4.2 在较小步长上限下优化S1

我们再来看看如果把步长上限设得很小，即使用opt(maxstep=3,notrust)，从FC结构出发优化S1态是什么情况。输入文件是文件包里的S1_step3.gjf

还是把输出文件中含有"Excited State 1"和"Excited State 2"的行里面的激发能都提取出来并绘制，得到的图如下所示。

从图上可以看出这回确实是走了透热态的路径，优化经过第9步结构附近的交叉点后，对应"Excited State 1"的黑色曲线就不再是能量最低的态了。这张图里的交叉点位置和上一张图里的交叉点位置基本相同，都是3.37eV的地方。

下面是优化过程第一步输出的信息
Excited State   1:      Singlet-A      4.8092 eV 257.81 nm f=0.0488 <S**2>=0.000
      29 -> 30         0.69464
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -394.332374034
Copying the excited state density for this state as the 1-particle RhoCI density.

Excited State   2:      Singlet-A      4.9900 eV 248.47 nm f=0.0019 <S**2>=0.000
      26 -> 30        -0.32031
      27 -> 30        -0.20046
      28 -> 30         0.59079

Excited State   3:      Singlet-A      5.3909 eV 229.99 nm f=0.0006 <S**2>=0.000
      26 -> 30         0.61783
      27 -> 30        -0.15704
      28 -> 30         0.28651

...略

下面是优化过程最后一步输出的信息
Excited State   1:      Singlet-A      3.2680 eV 379.39 nm f=0.0122 <S**2>=0.000
      29 -> 30        -0.70445
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -394.357141147
Copying the excited state density for this state as the 1-particle RhoCI density.

Excited State   2:      Singlet-A      3.2250 eV 384.45 nm f=0.0000 <S**2>=0.000
      28 -> 30         0.70662

Excited State   3:      Singlet-A      4.5729 eV 271.13 nm f=0.0024 <S**2>=0.000
      26 -> 30        -0.69564
      27 -> 30        -0.10455
...略
由于"This state for optimization and/or second-order correction"是对"Excited State   1"标注的，因此程序是对"Excited State   1"来计算受力/Hessian从而优化结构的（当然这是必然的，因为我们设的就是root=1）。

由以上信息可见，程序输出的时候总是按照Excited State 1,2,3,4...这样的次序输出的，但由于中途经历了势能面交叉，而且这次又成功地跟踪了S1透热态，因此到最后的结构下，被优化的对象"Excited State 1"的激发能已经变得高于"Excited State 2"了。另外，如组态系数体现的，"Excited State 1"是MO29->MO30跃迁，即HOMO->LUMO跃迁，如果你看一下这个结构下的这俩轨道的话，会发现这俩轨道都是pi轨道，这点也和FC结构下S1是pi-pi*跃迁完全对应。

在实际中，并非碰上没有顺利跟踪透热态的时候用小步长上限就总能解决问题，有的时候由于巧合，可能小步长上限的时候在交叉点附近误走上了绝热态，而用默认步长上限时反倒正确跟踪了透热态。

上一节我们原本想优化到S1透热态极小点，却“误”被优化到了第一绝热态极小点上，实际上也可以尝试补救，也就是在这个第一绝热态极小点上用TD(root=2)去优化在当前结构下应当是第2激发态的S1透热态。这个任务的输出文件是文件包里的S1_reopt.out，可以看到重新优化后，确实得到了S1透热态极小点，结构与本节我们得到的完全相同。

4.3 对S2的优化

再来看看对胞嘧啶的S2优化的情况。我们以FC结构作为起点，使用opt(maxstep=3,notrust) TD(nstates=5,root=2)关键词来做，计算级别同前。输入文件是文件包里的S2_step3.gjf。

还是将优化过程的"Excited State 1"和"Excited State 2"的激发能随优化步数的变化作图，如下所示

可见这次优化也经历了交叉点，是沿着S2透热态走的，因此红线在一开始是能量第二低的态，到了交叉点右侧就变成了能量最低的态了。但是，这次经历的交叉点和上一节的是不同，这次交叉点的位置是大约4.385 eV的位置，而之前经历的都是3.37eV的位置。为何会有区别？实际上S1和S2透热态之间的交叉实际上是个交叉缝（在一个高维空间内处处能量相同），有无数多个相交的位置，由于上一节的优化一开始是按照S1透热态的受力/Hessian移动的结构，而这一节是按照S2透热态的受力/Hessian进行的移动，因此经历了交叉缝的不同位置。

上一节两个任务优化出的结构，以及这一节优化出的最终结构（都无虚频）是各不相同的，结构如下

可见当前我们直接优化S2得到的最终结构相当扭曲，在这个结构下，这个态可以用NTO29->NTO30完美描述，这俩轨道如下所示

可见这个跃迁是n->pi*跃迁，如前所述这也正是FC结构下S2态的跃迁方式，进一步表明我们这一节的优化从始至终是在S2透热势能面上进行的。

由于S1和S2的交叉缝是高维的，因此从FC结构开始，沿着S1透热态的受力/Hessian行进，以及按照S2透热态的受力/Hessian行进，我们经历了不同的交叉点位置。而且又由于此体系S2透热态上有不同的极小点，因此本节一直沿着S2透热态走（称为a过程），以及上一节起初沿着S1透热态走但是中途因算法问题在交叉点处切换到了S2透热态（称为b过程），最终得到的两个S2透热态极小点结构是不同的。根据之前给出的NTO图，可以知道FC结构下的S2对应的n->pi*跃迁中孤对电子同时明显来自于O和N，而a过程最终优化出的是n(N)->pi*态的极小点，b过程则优化出的是n(O)->pi*态的极小点。

另外，如果本节在优化S2时用默认步长上限，我们会发现优化出的结构和用maxstep=3的时候略有不同（输出文件是文件包里的S2_defstep.out），不过差异非常小，对应于由于NH2朝向的不同所造成的两个特征很接近的n(N)->pi*跃迁的极小点。之所以步长上限的不同导致了优化出了这两个不同结构，必定是S2透热态势能面存在分叉，步长上限不同时由于巧合而恰好走了不同路径。有兴趣的读者可以在gview里打开S2_step3.out和S2_defstep.out仔细对比一下优化过程。

5 总结

激发态的优化比基态的优化复杂很多。由于激发态能级分布密集，优化过程经常经过势能面交叉区域，而且既有可能走透热路径也有可能走绝热路径，再加上激发态势能面又可能分叉、联通不同极小点，因此不光是计算级别会影响最终得到的结果，就连一些细碎的数值方面的设定诸如步长上限的差异都可能导致最终优化到不同结构上去，因此头脑里必须有清楚的势能面的概念、有对势能面交叉问题的正确理解。如果能把本文的胞嘧啶这个简单例子里的讨论、分析方法都彻底弄明白，对其它更复杂的体系优化激发态时若遇到一些令人困惑的结果，也应该不难搞清楚到底是怎么回事了。

↧

考察SAPT能量分解的能量项随分子二聚体间距变化的简单方法

March 3, 2019, 2:03 pm

≫ Next: 2018年度完结动画总评

≪ Previous: 谈谈势能面交叉对激发态优化的影响

注：本文内容主要是写给一个外国合作者的看的，所以是用英文写的。

考察SAPT能量分解的能量项随分子二聚体间距变化的简单方法
A simple way to investigate the variation of SAPT energy decomposition terms with respect to molecular dimer separation

文/Sobereva@北京科音 2019-Mar-4

1 Foreward

The symmetry adapted perturbation theory (SAPT) is a rigorous and useful way of evaluating intermolecular interaction energy; more importantly, the SAPT interaction energy can be decomposed into various physical terms, which are very useful for understanding the nature of the interaction. PSI4 should be the best code for performing the SAPT calulation, because it is free, fast and relatively easy to use. PSI4 can be obtained from http://psicode.org. I assume readers have already known how to use the PSI4 and meantime PSI4 has been installed on the machine in correct way.

It is often interesting to examine variation of SAPT interaction terms with respect to molecular dimer separation. In very simple cases, such as scanning SAPT terms for Ar-Ar distance of Ar dimer, this can be done by properly making use the rule of PSI4 input file, see this file for example: http://sobereva.com/attach/469/Ar-Ar.inp. However, for most practical cases, e.g. scanning the O...H distance in H2O...HOH dimer, this purpose cannot be easily realized by only using single PSI4 input file. In present article, I will introduce a simple and general way of obtaining all SAPT terms with varying intermolecular distance. Specifically, the "distance" mentioned here denotes spacing of a pair of atoms between the two monomers, and in the variation process the orientation and structure of the monomers keep fixed. The method described in this article consists of three steps:
(1) Generating SAPT input files
(2) Running PSI4 in batch mode
(3) Extracting data and plotting them as curve map

Below I will take water dimer as instance to show how to do. We want to vary H2-O4 distance from 1.5 to 3.5 Angstrom with step size of 0.2, therefore there should be 10 steps.

All relevant files of the water dimer instance can be downloaded here: http://sobereva.com/attach/469/waterdimer.rar

2 Generating SAPT input files

I wrote a code named dimerscan, which is used to generate PSI4 SAPT input files at various intermolecular separations. This code can be downloaded here: http://sobereva.com/attach/469/dimerscan.rar.

In this package, the "dimerscan.exe" is executable file in Windows, the "dimerscan" is executable file in Linux, and "SAPT_template.inp" is template input file of PSI4 SAPT task, it will be loaded by dimerscan. You can manually change memory specification, basis set and keyword of SAPT task in this file, while other parts should keep unchanged without special reasons.
PS: In the template file, the SAPT level is SAPT2+(3)dmp2/aug-cc-pVTZ. According to the benchmark in J. Chem. Phys., 140, 094106 (2014), this level is able to predict binding energy in very high accuracy (usually close to CCSD(T)/aug-cc-pVTZ), therefore it is highly recommended for small dimers.

We first optimize structure of water dimer at reasonable level (e.g. B3LYP-D3(BJ)/def2-TZVP) via your favourite quantum chemistry code, then create a plain text file like below (this is content of the H2Odimer.txt in the waterdimer.rar package):

3 3
0 1 0 1
O                  1.21571500    0.00004000   -0.12596300
H                  0.26191400   -0.00018400    0.04416700
H                  1.62937300   -0.00025200    0.74021400
O                 -1.08643200   -0.00004600    0.11097100
H                 -1.46302100   -0.76572600   -0.33250500
H                 -1.46252900    0.76620800   -0.33193600

The first line is the number of atoms in monomer 1 and monomer 2, the second line is net charge and spin multiplicity of monomer 1 and monomer 2. The content starting from line 3 is dimer coordinate (in Angstrom).

Put the SAPT_template.inp file into the same folder of dimerscan executable file, then boot up dimerscan, input path of the H2Odimer.txt, and input:
2,4 // Index of the atom in monomer 1 (H2) and that in monomer 2 (O4). Their distance will be gradually changed in your specified way
1.5 // Initial distance of H2-O4
10 // Number of steps
0.2 // Stepsize

Now you will find totally 11 .inp files have been generated in current folder. The 0000.inp is PSI4 SAPT input file at initial distance, while 0001.inp, 0002.inp ... 0010.inp correspond to the structure of scan steps 1, 2 ... 10. You can also find a file named scan.xyz in current folder, it is a trajectory file containing all the 11 geometries. You can load it into VMD visualization program to check if the geometry variation meets our expectation. The animation of playing the scan.xyz is shown below, as you can clearly see the 11 geometries have been correctly generated.

As an example, the content of the generated 0002.inp is shown below. This file is easy to undertstand, the task use memory up to 2000MB, current H2-O4 distance is 1.9, as denoted by the "dimerdist" variable. After completing the SAPT2+(3)dmp2 energy evaluating, various terms are assigned to user-defined variables, and finally they are printed to the output file together in specific format.

memory 2000 MB

molecule dimer {
0 1
O      1.215715    0.000040   -0.125963
H      0.261914   -0.000184    0.044167
H      1.629373   -0.000252    0.740214
--
0 1
O     -1.635758    0.000010    0.138187
H     -2.012347   -0.765670   -0.305289
H     -2.011855    0.766264   -0.304720
}
dimerdist=    1.900000

set {
basis aug-cc-pVTZ
scf_type DF
freeze_core True
}

energy('sapt2+(3)dmp2')
E_disp = get_variable('SAPT DISP ENERGY') * psi_hartree2kcalmol
E_elst = get_variable('SAPT ELST ENERGY') * psi_hartree2kcalmol
E_exch = get_variable('SAPT EXCH ENERGY') * psi_hartree2kcalmol
E_ind = get_variable('SAPT IND ENERGY') * psi_hartree2kcalmol
E_tot = get_variable('SAPT TOTAL ENERGY') * psi_hartree2kcalmol

psi4.print_out("\n")
psi4.print_out(" Summary of SAPT result (kcal/mol)\n")
psi4.print_out(" Distance E_tot E_elst E_exch E_disp E_ind\n")
psi4.print_out("%s %6.3f %10.3f %10.3f %10.3f %10.3f %10.3f\n" % ("R=",dimerdist,E_tot,E_elst,E_exch,E_disp,E_ind))

3 Running the SAPT input files in batches

Now, put all the .inp files we just generated to a folder used for running PSI4 calculation, and then put this shell script into the this folder: http://sobereva.com/attach/469/psi4all.sh. Open this file by text editor, change the value after -n argument to actual number of CPU cores that you want to use to conduct PSI4 calculation. Next, enter this folder and run this command: ./psi4all.sh. This script will invoke "psi4" command to execute all .inp files in current folder in turn and produce output files with same name but contain .out suffix.

4 Extracting data and plotting them as curve map

After all SAPT calculations have finished, run this command to extract data from output files to result.txt file: grep "R= " *.out > result.txt

The content of result.txt is shown below. As can be seen from the .inp files, the values should be: distance, total binding energy, electrostatic term, exchange term, dispersion term and induction term.
0000.out:R= 1.500      0.536    -20.989     37.925     -6.180    -10.220
0001.out:R= 1.700     -3.769    -13.378     19.103     -4.034     -5.460
0002.out:R= 1.900     -4.923     -8.860      9.532     -2.660     -2.935
0003.out:R= 2.100     -4.798     -6.144      4.719     -1.771     -1.602
0004.out:R= 2.300     -4.223     -4.460      2.322     -1.189     -0.896
0005.out:R= 2.500     -3.552     -3.370      1.138     -0.805     -0.515
0006.out:R= 2.700     -2.932     -2.630      0.556     -0.551     -0.306
0007.out:R= 2.900     -2.407     -2.108      0.271     -0.381     -0.189
0008.out:R= 3.100     -1.979     -1.723      0.132     -0.267     -0.120
0009.out:R= 3.300     -1.636     -1.431      0.064     -0.190     -0.079
0010.out:R= 3.500     -1.363     -1.203      0.031     -0.137     -0.054

Next we plot the data as curve map via Origin program. Boot up Origin, directly dragging the result.txt into the Origin window to import it, properly specifying column names, and then plotting Line+Symbol map of various SAPT terms with respect to the distance values, you will eventually get below map.

From the map it can be seen that the minimum point of water dimer should occur around the position of R(H2-O4)=1.9 Angstrom. Electrostatic, dispersion and induction terms play attractive role, while repulsive effect purely comes from exchange term. All terms smoothly converge to zero with respect to increase of H2-O4 separation. The data also clearly shows that the H-bond in water dimer is completely dominated by electrostatic interaction irrespective of the dimer separation.

↧